
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TXĐ: D = R \ {-2}
Ta có: \(y'=\dfrac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{\left(x+2\right)^2}=\dfrac{-x^2-4x+5}{\left(x+2\right)^2}\)
\(y'=0\Rightarrow-x^2-4x+5=0\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)
⇒ Hàm số y đồng biến trên (-5, -2) và (-2, 1)
Hàm số y nghịch biến trên (-∞, -5) và (1, +∞)


Tập xác định \(x< \frac{1}{2}\)
Ta có : \(y'=1-\frac{2}{1-2x}=\frac{-1-2x}{1-2x}\Rightarrow y'=0\Leftrightarrow x=-\frac{1}{2}\)
Hàm số đồng biến trên \(\left(-\infty;-\frac{1}{2}\right)\)
Hàm số nghịch biến trên \(\left(-\frac{1}{2};\frac{1}{2}\right)\)


Xét hàm số:
y
=
4
-
x
2
x
+
3
m
TXĐ: R \ {−3m/2}
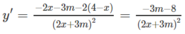
+) Nếu m < −8/3, y′ > 0 suy ra hàm số đồng biến trên các khoảng ![]()
+) Nếu m > −8/3, y′ < 0 suy ra hàm số nghịch biến trên các khoảng
![]()
+) Nếu m = −8/3 thì y = −1/2 khi x ≠ 4

TXĐ: `D=RR`
`y'=x^3-4x`
`y'=0 <=>` \(\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
\(\begin{array}{|l|cr|} \hline x & -\infty & & -2 &&&& & 0 & &&&&2&&& & +\infty\\ \hline y' & &-& 0& & &+& &0& &&-&&0& &&+&\\ \hline\end{array}\)
Vậy hàm số đồng biến trên các khoảng: `(-2;0)` và `(2; +\infty)`
Hàm số nghịch biến trên các khoảng: `(-\infty; -2)` và `(0;2)`.

TXĐ: (- ∞ ; 6 ) ∪ ( 6 ; + ∞ )
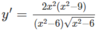
y’ = 0 ⇔ x = 3 hoặc x = -3
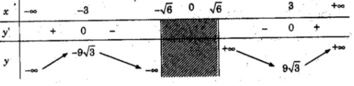
Vậy hàm số đồng biến trên các khoảng (- ∞ ; -3), (3; + ∞ ), nghịch biến trên các khoảng (-3; − 6 − 6 ), ( 6 ; 3).

TXĐ: [0; + ∞ )
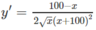
y’ = 0 ⇔ x = 100
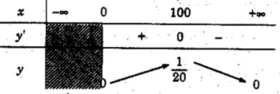
Vậy hàm số đồng biến trên khoảng (0; 100) và nghịch biến trên khoảng (100; + ∞ )

Ta có :\(y'=\left(6x-2\right)e^{3x^2-2x-x}\)
Hàm đồng biến trên \(\left(\frac{1}{3};+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;\frac{1}{3}\right)\)