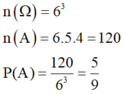Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giá còn lại của chiếc xe sau 5 năm sử dụng là:
\(680000000-55000000\cdot5=405000000\left(đồng\right)\)

Có \(7! = 5040\) cách sắp xếp 7 bạn ngồi vào 7 chiếc ghế \( \Rightarrow n\left( \Omega \right) = 5040\)
Gọi \(A\) là biến cố: “Bình vẫn ngồi đúng ghế cũ của mình”, \(B\) là biến cố “Minh vẫn ngồi đúng ghế cũ của mình”.
Vậy \(AB\) là biến cố “Cả Bình và Minh vẫn ngồi đúng ghế cũ của mình”, \(A \cup B\) là biến cố “Có ít nhất một trong hai bạn Bình và Minh vẫn ngồi đúng ghế cũ của mình”.
Xếp chỗ cho Bình ngồi đúng ghế cũ của mình có 1 cách.
Xếp chỗ cho 6 bạn còn lại có \(6! = 720\) cách.
\( \Rightarrow n\left( A \right) = 1.720 = 720 \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{720}}{{5040}} = \frac{1}{7}\)
Xếp chỗ cho Minh ngồi đúng ghế cũ của mình có 1 cách.
Xếp chỗ cho 6 bạn còn lại có \(6! = 720\) cách.
\( \Rightarrow n\left( B \right) = 1.720 = 720 \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left(\Omega \right)}} = \frac{{720}}{{5040}} = \frac{1}{7}\)
Xếp chỗ cho cả Bình và Minh ngồi đúng ghế cũ của mình có 1 cách.
Xếp chỗ cho 5 bạn còn lại có \(5! = 120\) cách.
\( \Rightarrow n\left( {AB} \right) = 1.120 = 120 \Rightarrow P\left( {AB} \right) = \frac{{n\left( {AB} \right)}}{{n\left( \Omega \right)}} = \frac{{120}}{{5040}} = \frac{1}{{42}}\)
\( \Rightarrow P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{1}{7} + \frac{1}{7} - \frac{1}{{42}} = \frac{{11}}{{42}}\)

Số tiền giảm đi là:
\(55000000\cdot5=275000000\left(đồng\right)\)
Giá tiền còn lại của chiếc xe sau 5 năm sử dụng là:
\(680000000-275000000=405000000\left(đồng\right)\)

Ít nhất 1 xe tốt, vậy nhiều nhất là 4 xe tốt :)
TH1: 1 xe tốt \(C^1_{10}.C^3_5\) (cách)
TH2: 2 xe tốt \(C^2_{10}.C^2_5\) (cách)
TH3: 3 xe tốt \(C^3_{10}.C^1_5\) (cách)
TH4: 4 xe tốt \(C^4_{10}.C^0_5\) (cách)
\(\Rightarrow n\left(A\right)=C^1_{10}.C^3_5+C^2_{10}.C^2_5+C^3_{10}.C^1_5+C^4_{10}.C^0_5=...\)
Không gian mẫu: \(n\left(\Omega\right)=C^4_{15}\)
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)

Đáp án B
Quay 3 lần thì số kết quả thu được là 103.
Kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay có số kết quả là 10.9.8 = 720
Xác suất để kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay là 720 10 3 = 18 25 = 0 , 72 .

Đáp án B
Số phần tử của không gian mẫu ![]() là
là ![]()
Gọi A là biến cố “chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau”, suy ra ![]()
Vậy xác suất cần tính là
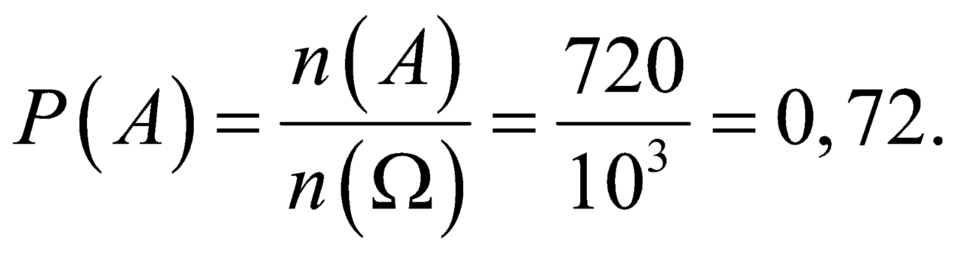

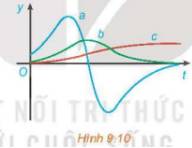
Hàm số c luôn đồng biến, tức là đạo hàm của nó phải luôn không âm, do đó hàm số b là đạo hàm của hàm số c; hàm số b đồng biến trên khoảng mà hàm số a dương và nghịch biến trên khoảng mà hàm số a âm, do đó hàm số a là đạo hàm của hàm số b.
Vậy hàm số a là hàm gia tốc, hàm số b là hàm vận tốc và hàm số c là hàm vị trí của ô tô.

Đáp án C
Phương pháp: Tính số phần tử của không gian mẫu và số phần tử của biến cố, sau đó suy ra xác suất.
Cách giải: Ba lần quay, mỗi lần chiếc kim có 7 khả năng dừng lại, do đó n Ω = 7 3 = 243
Gọi A là biến cố: “trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau" Khi đó ta có:
Lần quay thứ nhất, chiếc kim có 7 khả năng dừng lại.
Lần quay thứ hai, chiếc kim có 6 khả năng dừng lại.
Lần quay thứ ba, chiếc kim có 5 khả năng dừng lại.
Do đó nA = 7.6.5 = 210
Vậy
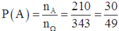

Đáp án B
A: ‘trong 3 lần quay, chiếc kim của bánh xe lần lượt dừng lại ở 3 vị trí khác nhau .’