Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Tính số phần tử của không gian mẫu và số phần tử của biến cố, sau đó suy ra xác suất.
Cách giải: Ba lần quay, mỗi lần chiếc kim có 7 khả năng dừng lại, do đó n Ω = 7 3 = 243
Gọi A là biến cố: “trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau" Khi đó ta có:
Lần quay thứ nhất, chiếc kim có 7 khả năng dừng lại.
Lần quay thứ hai, chiếc kim có 6 khả năng dừng lại.
Lần quay thứ ba, chiếc kim có 5 khả năng dừng lại.
Do đó nA = 7.6.5 = 210
Vậy
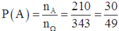

Đáp án B
Số phần tử không gian mẫu bằng 7 3 và số kết quả thuận lợi cho biến cố bằng 7.6.5
và xác suất cần tính bằng 7 . 6 . 5 7 3 = 30 49

Đáp án B
Số phần tử của không gian mẫu ![]() là
là ![]()
Gọi A là biến cố “chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau”, suy ra ![]()
Vậy xác suất cần tính là
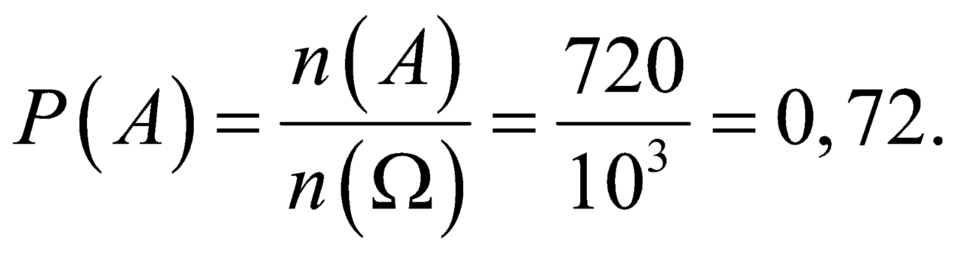

Mỗi lần quay bánh xe dừng lại ở 1 trong 7 vị trí: n(Ω) = 73=343.
Trong 3 lần quay kim của bánh xe lần lượt dừng lại ở 3 vị trí khác nhau nên ta có : n(X) = \(A^3_7\)= 210.
=> Xác xuất của 3 lần quay là: P=\(\dfrac{n\left(X\right)}{n\left(\Omega\right)}\)=\(\dfrac{30}{49}\)

Đáp án B
Quay 3 lần thì số kết quả thu được là 103.
Kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay có số kết quả là 10.9.8 = 720
Xác suất để kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay là 720 10 3 = 18 25 = 0 , 72 .

* 7.7.7 = 73 = 343
* \(A\frac{3}{7}=210\)
Do đó : \(P\left(A\right)=\frac{210}{343}=\frac{30}{49}\)
cậu giải được bài này thì cậu học 11 = tuổi Bình , vậy sao xưng chị (phía trên )?+!
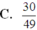
Đáp án B
A: ‘trong 3 lần quay, chiếc kim của bánh xe lần lượt dừng lại ở 3 vị trí khác nhau .’