KC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
G
3 tháng 3 2019
\(x^{2010}+y^{2010}=x^{2011}+y^{2011}=x^{2012}+y^{2012}\)
\(\Leftrightarrow x^{2010}+x^{2012}-2x^{2011}+y^{2010}+y^{2012}-2y^{2011}=0\)
\(\Leftrightarrow x^{2010}\left(x^2-2x+1\right)+y^{2010}\left(y^2-2y+1\right)=0\)
\(\Leftrightarrow x^{2010}\left(x-1\right)^2+y^{2010}\left(y-1\right)^2=0\)
\(x^{2010};y^{2010}>0\Leftrightarrow x=y=1.\Rightarrow x^{2016}+y^{2016}=2\)
2 tháng 4 2020
\(x^{2010}+y^{2010}=x^{2011}+y^{2011}=x^{2012}+y^{2012}\)
\(\Leftrightarrow x^{2010}+x^{2012}-2x^{2011}+y^{2010}+y^{2012}-2y^{2011}=0\)
\(\Leftrightarrow x^{2010}\left(x^2-2x+1\right)+y^{2010}\left(y^2-2y+1\right)=0\)
\(\Leftrightarrow x^{2010}\left(x-1\right)^2+y^{2010}\left(y-1\right)^2=0\)
\(x^{2010};y^{2010}>0\Leftrightarrow x=y=1.\Rightarrow x^{2016}+y^{2016}=2\)
...................................................................................................................
DT
0
PT
2
6 tháng 10 2017
Giải
Đặt x^1000 =a, y^1000=b
ta có a+b=6912
a^2+b^2=3376244
cần tính a^3+b^3= (a+b)(a^2-ab+b^2). chỉ còn thiếu ab nữa xong.
mà ab= [(a+b)^2 -(a^2+b^2)]/2.
Vậy a^3+b^3= (a+b) [ 3(a^2+b^2)/2 + (a+b)^2 /2 ]. thay vào là tính dc
MN
8 tháng 10 2017
Bạn cũng thi casio à? Mình cũng thi, lúc sáng mới khảo sát trúng bài này đơ luôn 
CM
20 tháng 5 2017
Đặt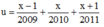 
Suy ra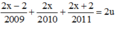 
Phương trình đã cho trở thành:
0,05.2u = 3,3 − u ⇔ 0,1u = 3,3 – u ⇔ 1,1u = 3,3 ⇔ u = 3.
Do đó: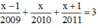 
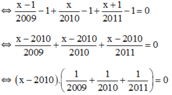
⇔ x – 2010 = 0
⇔ x = 2010.
Đặt a=x^670 b=y^670 tta có a+b=6.912 và a2 +b2=33.76244
suy ra a3 + b3=x^2013+y^2010suy ra(a+b)2=6.9122
a^2+2ab+b^2=47.775744 suy ra ab=7.006652
a^3+b^3=x^2010+y^2010=(a+b)(a^2-ab+b^2)=6.912*(33.76244+7.006652)=281.7959639
bạn tính lại nhé