Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(\dfrac{6\left(16x+3\right)}{7}-8=\dfrac{3\left(16x+3\right)}{7}+7\)
\(\Leftrightarrow6\left(16x+3\right)-56=3\left(16x+3\right)+49\)
\(\Leftrightarrow96x+18-56-48x-9-49=0\)
\(\Leftrightarrow48x=96\)
\(\Leftrightarrow x=2\)
Vậy phương trình đã cho có nghiệm x=2
a) Đặt u = \(\dfrac{16x+3}{7}\), ta có:
\(\dfrac{6\left(16x+3\right)}{7}\) - 8 = \(\dfrac{3\left(16x+3\right)}{7}\) + 7
<=> 6.u - 8 = 3.u + 7
=> 6.u - 3.u = 8 + 7
=> 3.u = 15
=> u = 15 / 3
=> u = 5
<=> \(\dfrac{16x+3}{7}\) = 5
=> 16x + 3 = 5 . 7
=> 16x = 35 - 3
=> 16x = 32
=> x = 32 / 16
=> x = 2
Vậy S = { 2 }.



\(\frac{x+1}{2011}+\frac{x+2}{2010}=\frac{x+3}{2009}+\frac{x+4}{2008}\Leftrightarrow\frac{x+1}{2011}+1+\frac{x+2}{2010}+1=\frac{x+3}{2009}+1+\frac{x+4}{2008}+1\)
\(\Leftrightarrow\frac{x+1}{2011}+\frac{2011}{2011}+\frac{x+2}{2010}+\frac{2010}{2010}=\frac{x+3}{2009}+\frac{2009}{2009}+\frac{x+4}{2008}+\frac{2008}{2008}\)
\(\Leftrightarrow\frac{x+1+2011}{2011}+\frac{x+2+2010}{2010}=\frac{x+3+2009}{2009}+\frac{x+4+2008}{2008}\)
\(\Leftrightarrow\frac{x+2012}{2011}+\frac{x+2012}{2010}=\frac{x+2012}{2009}+\frac{x+2012}{2008}\)
\(\Leftrightarrow\left(x+2012\right)\left(\frac{1}{2011}+\frac{1}{2010}\right)=\left(x+2012\right)\left(\frac{1}{2009}+\frac{1}{2008}\right)\)
\(\Leftrightarrow\left(x+2012\right)\left(\frac{1}{2011}+\frac{1}{2010}-\frac{1}{2009}-\frac{1}{2008}=0\right)\)
mà 1/2011+1/2010-1/2009-1/2008 khác 0
\(\Rightarrow x+2012=0\Rightarrow x=-2012\)
\(\left(3x-2\right)^2-x\left(9x-2\right)=24\Leftrightarrow9x^2-12x+4-9x^2+2x=24\)
\(\Leftrightarrow-10x+4=24\Leftrightarrow-10x=20\Leftrightarrow x=-2\)
1; Ta có : x+1/2011 + x+2/2010 = x+3/2009 + x+4/ 2008
Suy ra: 2+(x+1/2011 + x+2/2010 ) = 2+( x+3/2009 + x+4/2008)
suy ra ban tach 2=1+1 roi cong 1 voi tưng phân số trên nha sẽ ra kết quả ngay thôi
2; gợi ý nè : (3x-2)^2 =(3x)^2 + 2*3x*2+2^2

a) \(x^3-6x^2-9x+14=0\)
\(\Leftrightarrow x^3-8x^2+2x^2+7x-16x+14=0\)
\(\Leftrightarrow\left(x^3-8x^2+7x\right)+\left(2x^2-16x+14\right)=0\)
\(\Leftrightarrow x\left(x^2-8x+7\right)+2\left(x^2-8x+7\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-8x+7\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-7x-x+7\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[x\left(x-7\right)-\left(x-7\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)\left(x-7\right)=0\)
\(\Leftrightarrow x\in\left\{-2;1;7\right\}\)

\(\frac{x-1}{2013}+\frac{x-2}{2012}+\frac{x-3}{2011}=\frac{x-4}{2010}+\frac{x-5}{2009}+\frac{x-6}{2008}\)
\(\Leftrightarrow\)\(\left(\frac{x-1}{2013}-1\right)+\left(\frac{x-2}{2012}-1\right)+\left(\frac{x-3}{2011}-1\right)=\left(\frac{x-4}{2010}-1\right)+\left(\frac{x-5}{2009}-1\right)+\left(\frac{x-6}{2008}-1\right)\)
\(\Leftrightarrow\frac{x-2014}{2013}+\frac{x-2014}{2012}+\frac{x-2013}{2011}=\frac{x-2014}{2010}+\frac{x-2014}{2009}+\frac{x-2014}{2008}\)
\(\Leftrightarrow\left(x-2014\right)\left(\frac{1}{2013}+\frac{1}{2012}+\frac{1}{2011}-\frac{1}{2010}-\frac{1}{2009}-\frac{1}{2008}\right)=0\)
tự làm nốt~
kudo shinichi làm sai ở chỗ:
\(\frac{x-2013}{2011}\)phải là \(\frac{x-2014}{2011}\)mới đúng nhé

pt <=> (2-x/2009 + 1) = (1-x/2010 + 1) + (1 - x/2011)
<=> 2011-x/2009 = 2011-x/2010 + 2011-x/2011
<=> 2011-x/2009 - 2011-x/2010 - 2011-x/2011 = 0
<=> (2011-x).(1/2009-1/2010-1/2011) = 0
<=> 2011-x=0 ( vì 1/2009-1/2010-1/2011 khác 0 )
<=> x=2011
Vậy x=2011
Tk mk nha

\(\frac{x}{2008}+\frac{x+1}{2009}+...+\frac{x+4}{2012}=5\)
\(\Leftrightarrow\left(\frac{x}{2008}-1\right)+\left(\frac{x+1}{2009}-1\right)+...+\left(\frac{x+4}{2012}-1\right)=0\)
\(\Leftrightarrow\frac{x-2008}{2008}+\frac{x-2008}{2009}+...+\frac{x-2008}{2012}=0\)
\(\Leftrightarrow\left(x-2008\right)\left(\frac{1}{2008}+\frac{1}{2009}+..+\frac{1}{2012}\right)=0\)
Mà \(\left(\frac{1}{2008}+\frac{1}{2009}+..+\frac{1}{2012}\right)\ne0\)
Nên \(x-2008=0\)
\(\Leftrightarrow x=2008\)
Vậy : \(x=2008\)
\(\frac{x}{2008}+\frac{x+1}{2009}+\frac{x+2}{2010}+\frac{x+3}{2011}+\frac{x+4}{2012}=5\)
\(\Leftrightarrow\frac{x}{2008}+\frac{x+1}{2009}+\frac{x+2}{2010}+\frac{x+3}{2011}+\frac{x+4}{2012}-5=0\)
\(\Leftrightarrow\left(\frac{x}{2008}-1\right)+\left(\frac{x+1}{2009}-1\right)+\left(\frac{x+2}{2010}-1\right)+\left(\frac{x+3}{2011}-1\right)+\left(\frac{x+4}{2012}-1\right)=0\)
\(\Leftrightarrow\frac{x-2008}{2008}+\frac{x-2008}{2009}+\frac{x-2008}{2010}+\frac{x-2008}{2011}+\frac{x-2008}{2012}=0\)
\(\Leftrightarrow\left(x-2008\right)\left(\frac{1}{2008}+\frac{1}{2009}+\frac{1}{2010}+\frac{1}{2011}+\frac{1}{2012}\right)=0\)
Vì \(\frac{1}{2008}+\frac{1}{2009}+\frac{1}{2010}+\frac{1}{2011}+\frac{1}{2012}\ne0\)
\(\Rightarrow x-2008=0\)\(\Leftrightarrow x=2008\)
Vậy \(x=2008\)
Đặt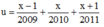
Suy ra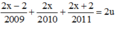
Phương trình đã cho trở thành:
0,05.2u = 3,3 − u ⇔ 0,1u = 3,3 – u ⇔ 1,1u = 3,3 ⇔ u = 3.
Do đó: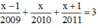
⇔ x – 2010 = 0
⇔ x = 2010.