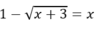K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
22 tháng 7 2021
Ta có :
\(x^2-(8m+1)x+15m^2+3m\leq 0 \\ \Leftrightarrow (x-3m)(x-5m-1) \leq 0\\ \Leftrightarrow x\in [3m;5m-1] \ hoặc \ x\in[5m-1;3m] \)
Độ dài của S trên trục số là:
\(|5m-1-3m|>3 \\ \Leftrightarrow |2m-1| > 3 \\ \Leftrightarrow 2m-1 > 3 \ hoặc \ 2m-1 <-3\\\Leftrightarrow m>2 \ hoặc\ m<-1\)
CM
19 tháng 9 2017
Đáp án: D
Điều kiện xác định của phương trình x - 1 x 2 - 4 = 3 - x
3 - x ≥ 0 x 2 - 4 ≠ 0 ⇔ x ≤ 3 x ≠ ± 2
HD
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 2 2021
\(\Leftrightarrow\dfrac{\left|x+2\right|}{x}\le3\)
- Với \(x< 0\) BPT \(\Rightarrow\dfrac{\left|x+2\right|}{x}< 0\) hiển nhiên đúng
- Với \(x>0\Rightarrow x+2>0\) BPT tương đương:
\(\dfrac{x+2}{x}\le3\Leftrightarrow x+2\le3x\Rightarrow x\ge1\)
Vậy \(\left[{}\begin{matrix}x< 0\\x\ge1\end{matrix}\right.\)
NT
2
PT
1
CM
16 tháng 11 2019
x ≥ 2 và x ≤ -4. Không có số thực x nào thỏa mãn điều kiện của phương trình.
CM
19 tháng 6 2019
Để phương trình x 2 + y 2 − 2 ( m − 3 ) x − 2 ( 2 m + 1 ) y + 3 m + 10 = 0 là phương trình của một đường tròn thì
m − 3 2 + 2 m + 1 2 − 3 m − 10 > 0
⇔ m 2 − 6 m + 9 + 4 m 2 + 4 m + 1 − 3 m − 10 > 0
5 m 2 − 5 m > 0 ⇔ m ∈ − ∞ ; 0 ∪ 1 ; + ∞
Đáp án B