HD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BT
8 tháng 5 2017
Đkxđ: \(\left\{{}\begin{matrix}5-x\ge0\\x-10>0\\\left(x-4\right)\left(x+5\right)\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\le5\\x>10\\x\ne4\\x\ne-5\end{matrix}\right.\)\(\Leftrightarrow x\in\varnothing\).
Vậy BPT vô nghiệm.
AH
Akai Haruma
Giáo viên
25 tháng 3 2021
Câu 1: ĐK: $x\neq -1$
Nếu $x\geq 0$ thì:
BPT \(\Leftrightarrow -2\leq \frac{2-3x}{x+1}\leq 2\Rightarrow \left\{\begin{matrix} x\leq 4\\ x\geq 0\end{matrix}\right.\Rightarrow x\in\left\{0;1;2;3;4\right\}\)
Nếu $x< 0$ thì:
BPT \(\Leftrightarrow -2\leq \frac{2+3x}{x+1}\leq 2\)
Trường hợp $-1< x< 0$ thì $\Leftrightarrow -2(x+1)\leq 2+3x\leq 2(x+1)$
$\Leftrightarrow x\geq \frac{-4}{5}$ và $x\leq 0$. Kết hợp với ĐK $-1< x< 0$ nên không có giá trị $x$ nguyên thỏa mãn
Trường hợp $x< -1$ thì $\Leftrightarrow -2(x+1)\geq 2+3x\geq 2(x+1)$
$\Leftrightarrow x\leq \frac{-4}{5}$ và $x\geq 0$ (vô lý)
Do đó có 5 giá trị $x$ nguyên thỏa mãn.
Đáp án B
AH
Akai Haruma
Giáo viên
25 tháng 3 2021
Câu 2:
VTCP của $\Delta_1$: $\overrightarrow{u_1}(m+1, -1)$
VTPT của $\Delta_2$: $\overrightarrow{n_2}(m,-6)$
Để 2 đường thẳng song song với nhau thì: $\overrightarrow{u_1}\perp \overrightarrow{n_2}$
$\Leftrightarrow m(m+1)+(-1)(-6)=0$
$\Leftrightarrow m^2+m+6=0$
$\Leftrightarrow (m+\frac{1}{2})^2=-\frac{23}{4}< 0$ (vô lý- loại)
Vậy không có giá trị m thỏa mãn
Đáp án B.
TL
0
15 tháng 4 2017
a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
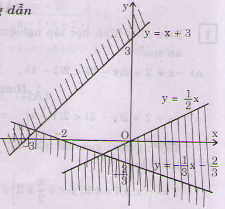
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
TH
0
HP
21 tháng 1 2021
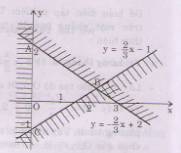
a, \(\left|3x+1\right|>2\)
\(\Leftrightarrow\left(\left|3x+1\right|\right)^2>4\)
\(\Leftrightarrow9x^2+6x+1>4\)
\(\Leftrightarrow9x^2+6x-3>0\)
\(\Leftrightarrow3\left(3x-1\right)\left(x+1\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{1}{3}\\x< -1\end{matrix}\right.\)
b, \(\left|2x-1\right|\le1\)
\(\Leftrightarrow\left(\left|2x-1\right|\right)^2\le1\)
\(\Leftrightarrow4x^2-4x+1\le1\)
\(\Leftrightarrow4x\left(x-1\right)\le0\)
\(\Leftrightarrow0\le x\le1\)
HP
21 tháng 1 2021
c, ĐK: \(x\ne13\)
\(\left|\dfrac{2}{x-13}\right|>\dfrac{8}{9}\)
\(\Leftrightarrow\dfrac{1}{\left|x-13\right|}>\dfrac{4}{9}\)
\(\Leftrightarrow4\left|x-13\right|< 9\)
\(\Leftrightarrow16\left(x^2-26x+169\right)< 81\)
\(\Leftrightarrow16x^2-416x+2623< 0\)
\(\Leftrightarrow\dfrac{43}{4}< x< \dfrac{61}{4}\)
\(\Rightarrow\) Có hai giả trị thỏa mãn yêu cầu bài toán
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 2 2021
\(\Leftrightarrow\sqrt{-x^2-2x+15}-x^2-2x+15\le a+15\)
Đặt \(\sqrt{-x^2-2x+15}=t\ge0\)
Đồng thời ta có: \(\sqrt{-x^2-2x+15}=\sqrt{\left(x+5\right)\left(3-x\right)}\le\dfrac{1}{2}\left(x+5+3-x\right)=4\)
\(\Rightarrow0\le t\le4\)
BPT trở thành: \(t^2+t\le a+15\Leftrightarrow t^2+t-15\le a\) ; \(\forall t\in\left[0;4\right]\)
\(\Leftrightarrow a\ge\max\limits_{t\in\left[0;4\right]}\left(t^2+t-15\right)\)
Xét hàm \(f\left(t\right)=t^2+t-15\) trên \(\left[0;4\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{2}\notin\left[0;4\right]\) ; \(f\left(0\right)=-15\) ; \(f\left(4\right)=5\)
\(\Rightarrow f\left(t\right)_{max}=4\Rightarrow a\ge4\)
16 tháng 6 2023
a: =>(x-1)(3x-4)>0
=>x>4/3 hoặc x<1
b: =>x^3-3x^2-10x^2+30x+12x-36>0
=>(x-3)(x^2-10x+12)>0
Th1: x-3>0và x^2-10x+12>0
=>x>5+căn 13
TH2: x-3<0 và x^2-10x+12<0
=>x<3 và 5-căn 13<x<5+căn 13
=>3<x<5+căn 13
\(\Leftrightarrow\dfrac{\left|x+2\right|}{x}\le3\)
- Với \(x< 0\) BPT \(\Rightarrow\dfrac{\left|x+2\right|}{x}< 0\) hiển nhiên đúng
- Với \(x>0\Rightarrow x+2>0\) BPT tương đương:
\(\dfrac{x+2}{x}\le3\Leftrightarrow x+2\le3x\Rightarrow x\ge1\)
Vậy \(\left[{}\begin{matrix}x< 0\\x\ge1\end{matrix}\right.\)