HN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
JJ
1
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 12 2021
\(\dfrac{2019x}{xy+2019x+2019}+\dfrac{y}{yz+y+2019}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{2019xz}{xyz+2019xz+2019z}+\dfrac{xz.y}{xz.yz+xz.y+2019xz}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{2019xz}{2019+2019xz+2019z}+\dfrac{2019}{2019z+2019+2019xz}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{xz}{1+xz+z}+\dfrac{1}{z+1+xz}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{xz+z+1}{xz+z+1}=1\)
H9
HT.Phong (9A5)
CTVHS
28 tháng 6 2023
Bài 2:
1) \(x^2-4=x^2-2^2=\left(x-2\right)\left(x+2\right)\)
2) \(1-4x^2=1^2-\left(2x\right)^2=\left(1-2x\right)\left(1+2x\right)\)
3) \(4x^2-9=\left(2x\right)^2-3^2=\left(2x+3\right)\left(2x-3\right)\)
4) \(9-25x^2=3^2-\left(5x\right)^2=\left(3-5x\right)\left(3+5x\right)\)
5) \(4x^2-25=\left(2x\right)^2-5^2=\left(2x+5\right)\left(2x-5\right)\)
6) \(9x^2-36=\left(3x\right)^2-6^2=\left(3x-6\right)\left(3x+6\right)\)
7) \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)
8) \(x^2-\left(2y\right)^2=\left(x-2y\right)\left(x+2y\right)\)
9) \(\left(2x\right)^2-y^2=\left(2x-y\right)\left(2x+y\right)\)
10) \(\left(3x\right)^2-9y^4=\left(3x\right)^2-\left(3y^2\right)^2=\left(3x-3y^2\right)\left(3x+3y^2\right)\)
H9
HT.Phong (9A5)
CTVHS
28 tháng 6 2023
Bài 2:
21) \(\left(\dfrac{x}{3}-\dfrac{y}{4}\right)\left(\dfrac{x}{3}+\dfrac{y}{4}\right)=\left(\dfrac{x}{3}\right)^2-\left(\dfrac{y}{4}\right)^2=\dfrac{x^2}{9}-\dfrac{y^2}{16}\)
22) \(\left(\dfrac{x}{y}-\dfrac{2}{3}\right)\left(\dfrac{x}{y}+\dfrac{2}{3}\right)=\left(\dfrac{x}{y}\right)^2-\left(\dfrac{2}{3}\right)^2=\dfrac{x^2}{y^2}-\dfrac{4}{9}\)
23) \(\left(\dfrac{x}{2}+\dfrac{y}{3}\right)\left(\dfrac{x}{2}-\dfrac{y}{3}\right)=\left(\dfrac{x}{2}\right)^2-\left(\dfrac{y}{3}\right)^2=\dfrac{x^2}{4}-\dfrac{y^2}{9}\)
24) \(\left(2x-\dfrac{2}{3}\right)\left(\dfrac{2}{3}+2x\right)=\left(2x-\dfrac{2}{3}\right)\left(2x+\dfrac{2}{3}\right)=\left(2x\right)^2-\left(\dfrac{2}{3}\right)^2=4x^2-\dfrac{4}{9}\)
25) \(\left(2x+\dfrac{3}{5}\right)\left(\dfrac{3}{5}-2x\right)=\left(\dfrac{3}{5}+2x\right)\left(\dfrac{3}{5}-2x\right)=\left(\dfrac{3}{5}\right)^2-\left(2x\right)^2=\dfrac{9}{25}-4x^2\)
26) \(\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{4}{3}+\dfrac{1}{2}x\right)=\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{1}{2}x+\dfrac{4}{3}\right)=\left(\dfrac{1}{2}x\right)^2-\left(\dfrac{4}{3}\right)^2=\dfrac{1}{4}x^2-\dfrac{16}{9}\)
27) \(\left(\dfrac{2}{3}x^2-\dfrac{y}{2}\right)\left(\dfrac{2}{3}x^2+\dfrac{y}{2}\right)=\left(\dfrac{2}{3}x^2\right)^2-\left(\dfrac{y}{2}\right)^2=\dfrac{4}{9}x^4-\dfrac{y^2}{4}\)
28) \(\left(3x-y^2\right)\left(3x+y^2\right)=\left(3x\right)^2-\left(y^2\right)^2=9x^2-y^4\)
29) \(\left(x^2-2y\right)\left(x^2+2y\right)=\left(x^2\right)^2-\left(2y\right)^2=x^4-4y^2\)
30) \(\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x^2\right)^2-\left(y^2\right)^2=x^4-y^4\)
T
26 tháng 10 2023
1)
\((x+2)(x+3)(x+4)(x+5)-24\\=[(x+2)(x+5)]\cdot[(x+3)(x+4)]-24\\=(x^2+7x+10)(x^2+7x+12)-24\)
Đặt \(x^2+7x+10=y\), khi đó biểu thức trở thành:
\(y(y+2)-24\\=y^2+2y-24\\=y^2+2y+1-25\\=(y+1)^2-5^2\\=(y+1-5)(y+1+5)\\=(y-4)(y+6)\\=(x^2+7x+10-4)(x^2+7x+10+6)\\=(x^2+7x+6)(x^2+7x+16)\)
2) Bạn xem lại đề!
16 tháng 12 2022
\(Q=\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{x^2+y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2+2x^2+2y^2}{2\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{2x^2+2y^2+4xy}{2\left(x-y\right)\left(x+y\right)}=\dfrac{2\left(x+y\right)^2}{2\left(x-y\right)\left(x+y\right)}=\dfrac{x+y}{x-y}\)
26 tháng 7 2023
`B = x^2- 2xy + y^2 + 2x - 10y + 17
`2B = 2x^2 - 4xy + 2y^2 + 4x - 20y + 34`
`= (x-y)^2 + (x+2)^2 + (y-5)^2 + 5 >= 5`.
10 tháng 9 2023
a) \(x^2+xy+y^2+1\)
\(=x^2+xy+\dfrac{y^2}{4}-\dfrac{y^2}{4}+y^2+1\)
\(=\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1\)
mà \(\left\{{}\begin{matrix}\left(x+\dfrac{y}{2}\right)^2\ge0,\forall x;y\\\dfrac{3y^2}{4}\ge0,\forall x;y\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1>0,\forall x;y\)
\(\Rightarrow dpcm\)
10 tháng 9 2023
b) \(...=x^2-2x+1+4\left(y^2+2y+1\right)+z^2-6z+9+1\)
\(=\left(x-1\right)^2+4\left(y^{ }+1\right)^2+\left(z-3\right)^2+1>0,\forall x.y\)
\(\Rightarrow dpcm\)
27 tháng 9 2021
Xét tam giác ABC có:
M là trung điểm AB(gt)
N là trung điểm AC(gt)
=> MN là đường trung bình
\(\Rightarrow BC=2MN=2.5=10\left(cm\right)\)
V
22 tháng 7 2021
a. \(A=\left(4-5x\right)^2-\left(3+5x\right)^2\\ =\left(4-5x+3+5x\right)\left(4-5x-3-5x\right)\\ =7.\left(-5x\right)=-35x\)
b. \(B=\left(3x-1\right)\left(1+3x\right)-\left(3x+1\right)^2\\ =9x^2-1-\left(9x^2+6x+1\right)\\ =9x^2-1-9x^2-6x-1\\ =-6x-2\)
22 tháng 7 2021
a) Ta có: \(A=\left(4-5x\right)^2-\left(5x+3\right)^2\)
\(=\left(4-5x-5x-3\right)\left(4-5x+5x+3\right)\)
\(=7\left(-10x+1\right)\)
\(=-70x+7\)
b) Ta có: \(B=\left(3x-1\right)\left(3x+1\right)-\left(3x+1\right)^2\)
\(=\left(3x+1\right)\left(3x-1-3x-1\right)\)
\(=-2\left(3x+1\right)\)
\(=-6x-2\)
c) Ta có: \(C=\left(2x+5\right)^3-\left(2x-5\right)^3-\left(120x^2+49\right)\)
\(=8x^3+60x^2+150x+125-\left(8x^3-60x^2+150x-125\right)-120x^2-49\)
\(=8x^3-60x^2+150x+76-8x^3+60x^2-150x+125\)
\(=201\)
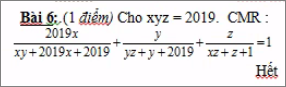
\(\Rightarrow x^2+y^2-3xxy=0\)
\(\Rightarrow x^2-2xy+y^2-xy=0\)
\(\Rightarrow\left(x-y\right)^2=xy\)
\(\Rightarrow x-y=\sqrt{xy}=\sqrt{x}.\sqrt{y}\)
\(\Rightarrow x=\sqrt{x}.\sqrt{y}+y=\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)\)
\(\Rightarrow y=x-\sqrt{x}.\sqrt{y}=\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)\)
\(\Rightarrow\frac{x}{y}=\frac{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}\)