
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 5:
a. $|x+\frac{4}{5}|-\frac{1}{7}=0$
$|x+\frac{4}{5}|=\frac{1}{7}$
$\Rightarrow x+\frac{4}{5}=\pm \frac{1}{7}$
$\Rightarrow x=\frac{-23}{35}$ hoặc $x=\frac{-33}{35}$
v.
$2x+5-(x-7)=18$
$2x+5-x+7=18$
$x+12=18$
$x=6$
c.
$2(x+1)+4^2=2^4$
$2(x+1)+16=16$
$2(x+1)=0$
$x+1=0$
$x=-1$
d.
$\frac{x-3}{x+5}=\frac{5}{7}$
$\Rightarrow 7(x-3)=5(x+5)$
$\Rightarrow 7x-21=5x+25$
$\Rightarrow 2x=46$
$\Rightarrow x=23$
Câu 5:
\(a,\left|x+\dfrac{4}{5}\right|-\dfrac{1}{7}=0\\ \Leftrightarrow\left|x+\dfrac{4}{5}\right|=\dfrac{1}{7}\\ \Leftrightarrow\left[{}\begin{matrix}x+\dfrac{4}{5}=\dfrac{1}{7}\\x+\dfrac{4}{5}=-\dfrac{1}{7}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{7}-\dfrac{4}{5}\\x=-\dfrac{1}{7}-\dfrac{4}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{23}{35}\\x=-\dfrac{33}{35}\end{matrix}\right.\\ b,2x+5-\left(x-7\right)=18\\ \Leftrightarrow2x-x=18-5-7\\ \Leftrightarrow x=6\\ c,2\left(x+1\right)+4^2=2^4\\ \Leftrightarrow2\left(x+1\right)=2^4-4^2=16-16\\ \Leftrightarrow2\left(x+1\right)=0\\ \Rightarrow x+1=0\\ \Leftrightarrow x=0-1=-1\\ d,\dfrac{x-3}{x+5}=\dfrac{5}{7}\left(x\ne-5\right)\\ \Leftrightarrow7\left(x-3\right)=5\left(x+5\right)\\ \Leftrightarrow7x-21=5x+25\\ \Leftrightarrow7x-5x=25+21\\ \Leftrightarrow2x=46\\ \Leftrightarrow x=23\)


2:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH=12cm
b: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
c: góc IAC+góc AED
=góc ICA+góc AHD
=góc ACB+góc ABC=90 độ
=>AI vuông góc ED
4:
a: góc BDH=góc BEH=góc DBE=90 độ
=>BDHE là hình chữ nhật
b: BDHE là hình chữ nhật
=>góc BED=góc BHD=góc A
Xét ΔBED và ΔBAC có
góc BED=góc A
góc EBD chung
=>ΔBED đồng dạng với ΔBAC
=>BE/BA=BD/BC
=>BE*BC=BA*BD
c: góc MBC+góc BED
=góc C+góc BHD
=góc C+góc A=90 độ
=>BM vuông góc ED

x + 1 = ( x + 1 )2
x + 1 = x2 + 2x + 1
x - 2x - x2 = - 1 + 1
- x - x2 = 0
- x ( x + 1) = 0
TH1: - x = 0 suy ra x = 0
TH2: x + 1 = 0 suy ra x = - 1
Vậy x = 0 hoặc x = - 1.

\(2x^2+5x-3=0\)
\(\Leftrightarrow2x^2-x+6x-3=0\)
\(\Leftrightarrow x\left(2x-1\right)+3\left(2x-1\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+3=0\\2x-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-3\\x=\frac{1}{2}\end{cases}}}\)

a: Xét ΔABC có
AM là đường trung tuyến
G là trọng tâm
Do đó: \(\dfrac{AG}{AM}=\dfrac{2}{3}\)
Xét ΔABM có DG//BM
nên \(\dfrac{AD}{AB}=\dfrac{AG}{AM}\)
=>\(\dfrac{AD}{AB}=\dfrac{2}{3}\)
b: Xét ΔAMC có GE//MC
nên \(\dfrac{AE}{AC}=\dfrac{AG}{AM}\)
=>\(\dfrac{AE}{AC}=\dfrac{2}{3}\)
=>\(AE=\dfrac{2}{3}AC\)
AE+EC=AC
=>\(EC+\dfrac{2}{3}AC=AC\)
=>\(EC=\dfrac{1}{3}AC\)
\(AE=\dfrac{2}{3}AC=2\cdot\dfrac{1}{3}\cdot AC=2\cdot EC\)

Bài 3:
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC


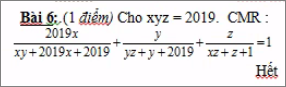



 giúp mik vs mik đag cần gấp
giúp mik vs mik đag cần gấp
 Giúp mik bài 4 vs mn, mik đag cần gấp
Giúp mik bài 4 vs mn, mik đag cần gấp
\(\dfrac{2019x}{xy+2019x+2019}+\dfrac{y}{yz+y+2019}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{2019xz}{xyz+2019xz+2019z}+\dfrac{xz.y}{xz.yz+xz.y+2019xz}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{2019xz}{2019+2019xz+2019z}+\dfrac{2019}{2019z+2019+2019xz}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{xz}{1+xz+z}+\dfrac{1}{z+1+xz}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{xz+z+1}{xz+z+1}=1\)