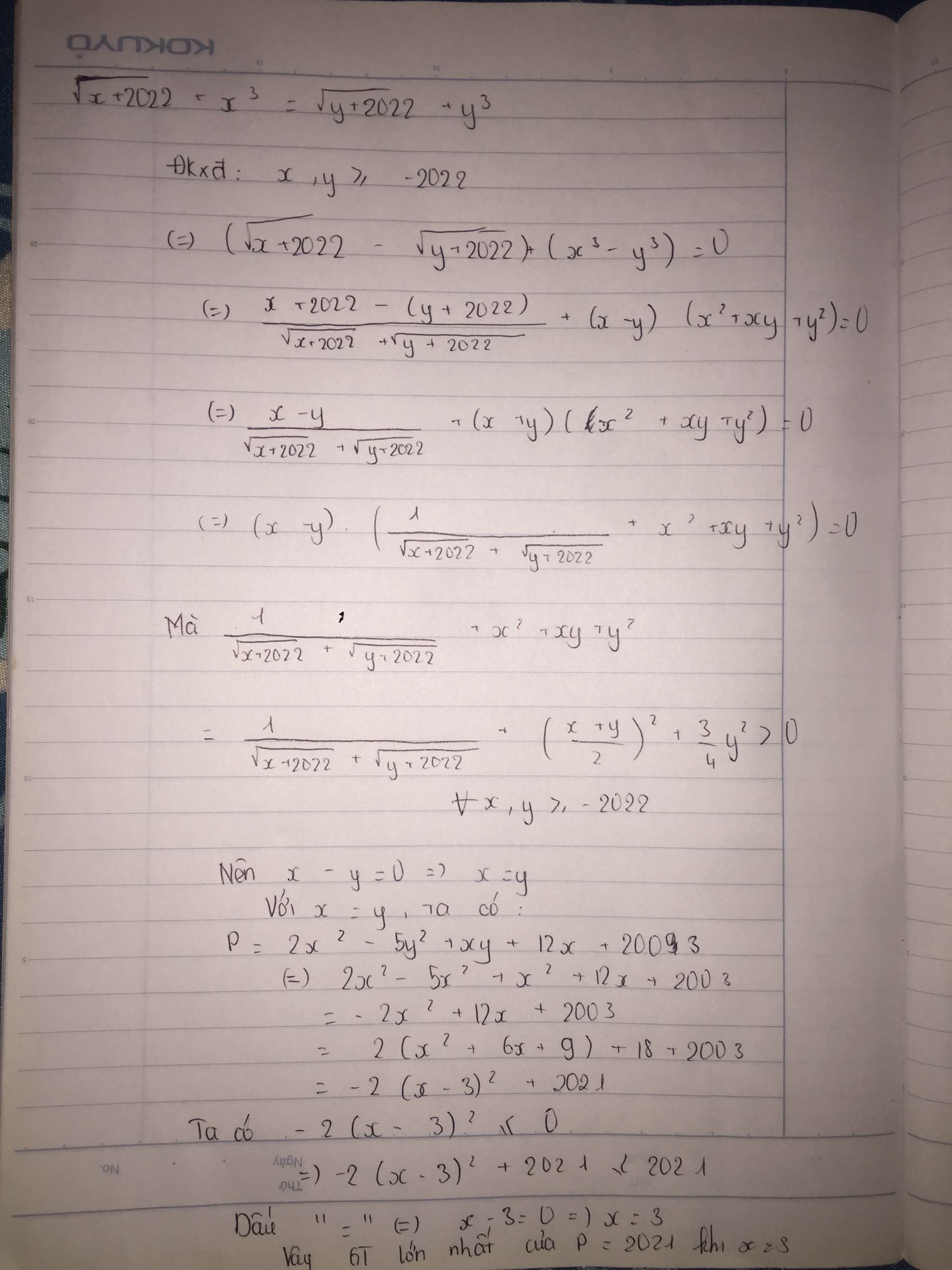K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DA
1
10 tháng 4 2023
\(\Leftrightarrow\left(\sqrt{x+2022}-\sqrt{y+2022}\right)+\left(x^3-y^3\right)=0\)
=>\(\dfrac{x-y}{\sqrt{x+2022}+\sqrt{y+2022}}+\left(x-y\right)\left(x^2+xy+y^2\right)=0\)
=>x-y=0
=>x=y
P=2x^2-5x^2+x^2+12x+2023
=-2x^2+12x+2023
=-2(x^2-6x-2023/2)
=-2(x^2-6x+9-2041/2)
=-2(x-3)^2+2041<=2041
Dấu = xảy ra khi x=3
TN
22 tháng 5 2016
1)Giả sử (x;y) là cặp số nguyên dương cần tìm. Khi đó ta có:
(xy-1) chia hết (x3+x) => (xy-1) chia hết x(x2+1) (1)
Do (x; xy-1) =1 ( Thật vậy: gọi (x;xy-1) =d => d chia hết x => d chia hết xy => d chia hết 1).
Nên từ (1) ta có:
(xy-1) chia hết (x2+1)
=> (xy-1) chia hết (x2+1+xy -1) => (xy-1) chia hết (x2+xy) => (xy-1) chia hết x(x+y) => (xy-1) chia hết (x+y)
Điều đó có nghĩa là tồn tại z \(\in\) N* sao cho:
x+y = z(xy-1) <=> x+y+z =xyz (2)
Do vai trò bình đẳng nên ta giả sử: x \(\ge\) y \(\ge\) z.
Từ (2) ta có: x+y+z \(\le\) 3x => 3x \(\ge\) xyz => 3 \(\ge\) yz \(\ge\) z2 => z=1
=> 3 \(\ge\) y => y \(\in\) {1;2;3}
Nếu y=1: x+2 =x (loại)
Nếu y=2: (2) trở thành x+3 =2x => x=3
Nếu y=3: x+4 = 3x => x=2 (loại vì ta có x\(\ge\)y)
Vậy khi x \(\ge\) y \(\ge\) z thì (2) có 1 nghiệm (x;y;z) là (3;2;1)
2)\(\Leftrightarrow\sqrt{12x^2-12x+7}+\sqrt{8x^2-8x+3}=-4x^2+4x+2\)
\(\Leftrightarrow\sqrt{12x^2-12x+7}+\sqrt{8x^2-8x+3}+4x^2-4x-2=0\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\frac{1}{2}\)
