
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(x^2-\dfrac{3}{2}=0\)
nên \(x^2=\dfrac{3}{2}\)
hay \(x\in\left\{\dfrac{\sqrt{6}}{2};-\dfrac{\sqrt{6}}{2}\right\}\)
b: \(\dfrac{1}{2}x^2+\dfrac{7}{2}x=0\)
\(\Leftrightarrow x^2+7x=0\)
=>x(x+7)=0
=>x=0 hoặc x=-7
c: \(2x\left(x-\dfrac{1}{7}\right)=0\)
=>x(x-1/7)=0
=>x=0 hoặc x=1/7
d: (3x-2)(2x-2/3)=0
=>3x-2=0 hoặc 2x-2/3=0
=>3x=2 hoặc 2x=2/3
=>x=2/3 hoặc x=1/3

\(x-\frac{7}{2}< 0\)
\(\Rightarrow x-\frac{7}{2}\) âm
\(\Rightarrow x< \frac{7}{2}\)
tíc mình nha

a) 5.(x-2)-3x.(x-2)=0
(x-2).(5-3x)=0
x-2=0 5-3x=0
x=2 x=5/3
b)6x.(x-7)-7x^2.(x-7)=0
(x-7).(6x-7x^2)=0
(x-7).x.(6-7x)=0
x-7=0 x=0 6-7x=0
x=7 x=6/7
a, 5 . ( x - 2 ) + 3x . ( 2 - x ) = 0
5 . ( x - 2 ) - 3x . ( x - 2 ) = 0
( 5 - 3x )( x - 2 ) = 0
=> 5 - 3x = 0 hoặc x - 2 = 0
=> x = 5/3 hoặc x = 2
b, 6x . ( x - 7 ) + 7x2. ( 7 - x ) = 0
6x . ( x - 7 ) - 7x2 . ( x - 7 ) = 0
( x - 7 )( 6x - 7x2 ) = 0
x . ( x - 7 )( 6 - 7x ) = 0
=> x = 0 hoặc x - 7 = 0 hoặc 6 - 7x = 0
=> x = 0 hoặc x = 7 hoặc x = 6/7

1) x (x-2016) + 2015 (2016-x) = 0
x (x-2016) - 2015 (x- 2016) = 0
(x-2015)(x-2016) =0
\(\Rightarrow\orbr{\begin{cases}x-2015=0\\x-2016=0\end{cases}\Rightarrow\orbr{\begin{cases}x=2015\\x=2016\end{cases}}}\)
Vậy x= 2015; 2016
2) -5x (x-15) + (15-x) = 0
-5x (x-15) - (x-15) =0
(-5x -1) (x-15) =0
\(\Rightarrow\orbr{\begin{cases}-5x-1=0\\x-15=0\end{cases}\Rightarrow\orbr{\begin{cases}-5x=1\\x=15\end{cases}\Rightarrow}\orbr{\begin{cases}x=-\frac{1}{5}\\x=15\end{cases}}}\)
Vậy x= -1/5; 15
3) 3x (3x-7) - (7-3x) =0
3x(3x-7) + (3x -7) =0
(3x+1) (3x-7) =0
\(\Rightarrow\orbr{\begin{cases}3x+1=0\\3x-7=0\end{cases}\Rightarrow\orbr{\begin{cases}3x=-1\\3x=7\end{cases}\Rightarrow}\orbr{\begin{cases}x=-\frac{1}{3}\\x=\frac{7}{3}\end{cases}}}\)
Vậy x= -1/3 ; 7/3


a) x÷0,(7)=0,(32):2,(4)
\(x:\frac{7}{9}=\frac{32}{99}:\frac{22}{9}\)
\(x:\frac{7}{9}=\frac{16}{121}\)
\(x=\frac{16}{121}.\frac{7}{9}\)
\(x=\frac{112}{1089}\)
b)0,(17):2,(3)=x:0,(3)
\(\frac{17}{99}:\frac{7}{3}=x:\frac{1}{3}\)
\(\frac{17}{231}=x:\frac{1}{3}\)
x=\(\frac{17}{231}.\frac{1}{3}\)
\(x=\frac{17}{693}\)

a, \(\left|x^2+2x\right|+\left|\left(x+2\right)\left(x-7\right)\right|=0\)
Dấu ''='' xảy ra khi : \(x^2+2x=0\)và \(\left(x+2\right)\left(x-7\right)=0\)
\(\Leftrightarrow x=0or-2andx=-2;7\)
Vậy \(x\in\left\{0;-2;7\right\}\)
b, tương tự

a)\(\left|2x-3y\right|+\left|2y-4z\right|=0\)
\(\left\{{}\begin{matrix}\left|2x-3y\right|\ge0\forall x;y\\\left|2y-4z\right|\ge0\forall y;z\end{matrix}\right.\) \(\Rightarrow\left|2x-3y\right|+\left|2y-4z\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|2x-3y\right|=0\\\left|2y-4z\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=3y\\2y=4z\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{2}\\\dfrac{y}{4}=\dfrac{z}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{6}=\dfrac{y}{4}\\\dfrac{y}{4}=\dfrac{z}{2}\end{matrix}\right.\)
\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{2}=\dfrac{x+y+z}{6+4+2}=\dfrac{7}{12}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{7}{12}.6=\dfrac{7}{2}\\y=\dfrac{7}{12}.4=\dfrac{7}{3}\\z=\dfrac{7}{12}.2=\dfrac{7}{6}\end{matrix}\right.\)
b)\(\left|x-2\right|+\left|x-3\right|+\left|x-4\right|=0\)
\(\left\{{}\begin{matrix}\left|x-2\right|\ge0\\\left|x-3\right|\ge0\\\left|x-4\right|\ge0\end{matrix}\right.\) \(\Leftrightarrow\left|x-2\right|+\left|x-3\right|+\left|x-4\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|x-2\right|=0\\\left|x-3\right|=0\\\left|x-4\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=3\\x=4\end{matrix}\right.\)
Vì \(2\ne3\ne4\) nên \(x\in\varnothing\)
c)
\(\left|x+1\right|+\left|x+2\right|+...+\left|x+8\right|+\left|x+9\right|\)
Với mọi \(x\ge0\) ta có:
\(\left\{{}\begin{matrix}\left|x+1\right|=x+1\\\left|x+2\right|=x+2\\\left|x+8\right|=x+8\\\left|x+9\right|=x+9\end{matrix}\right.\)\(\Leftrightarrow x+1+x+2+...+x+8+x+9=x-1\)
\(\Leftrightarrow9x+90=x-1\)
\(\Leftrightarrow9x=x-89\)
\(\Leftrightarrow-8x=89\)
\(\Leftrightarrow x=\dfrac{89}{-8}\left(KTM\right)\)
Với mọi \(x< 0\) ta có:
\(\left\{{}\begin{matrix}x+1=-x-1\\x+2=-x-2\\x+8=-x-8\\x+9=-x-9\end{matrix}\right.\) \(\Leftrightarrow\left(-x-1\right)+\left(-x-2\right)+...+\left(-x-8\right)+\left(-x-9\right)=x-1\)
\(\Leftrightarrow-9x-90=x-1\)
\(\Leftrightarrow-9x=x+89\)
\(\Leftrightarrow-10x=89\)
\(\Leftrightarrow x=\dfrac{89}{-10}\left(TM\right)\)
d)\(\left|2x-3y\right|+\left|5y-2z\right|+\left|2z-6\right|=0\)
\(\left\{{}\begin{matrix}\left|2x-3y\right|\ge0\\ \left|5y-2z\right|\ge0\\ \left|2z-6\right|\ge0\end{matrix}\right.\) \(\Leftrightarrow\left|2x-3y\right|+\left|5y-2z\right|+\left|2z-6\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|2x-3y\right|=0\\\left|5y-2z\right|=0\\\left|2z-6\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}z=3\\y=\dfrac{6}{5}\\x=\dfrac{9}{5}\end{matrix}\right.\)
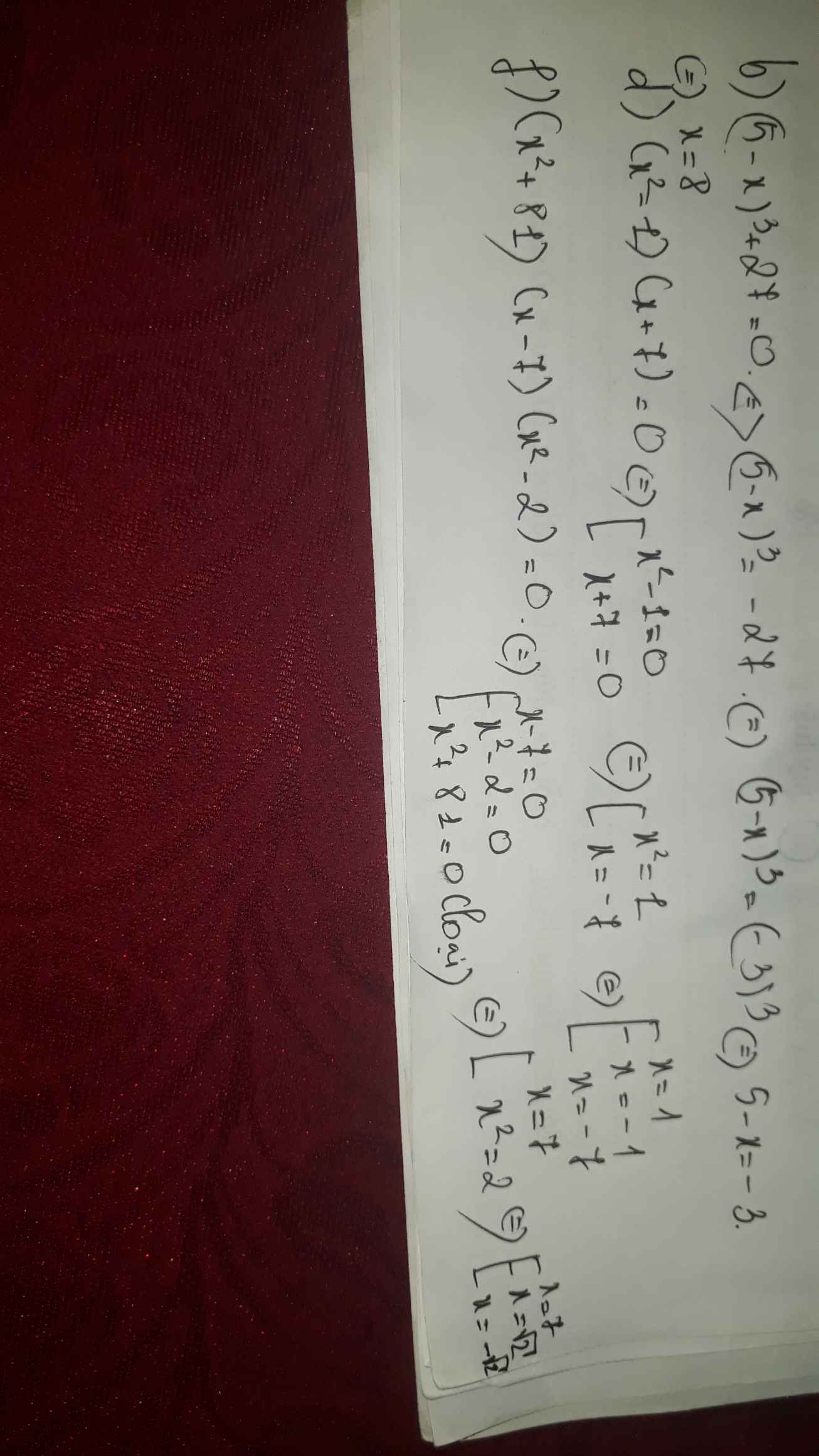
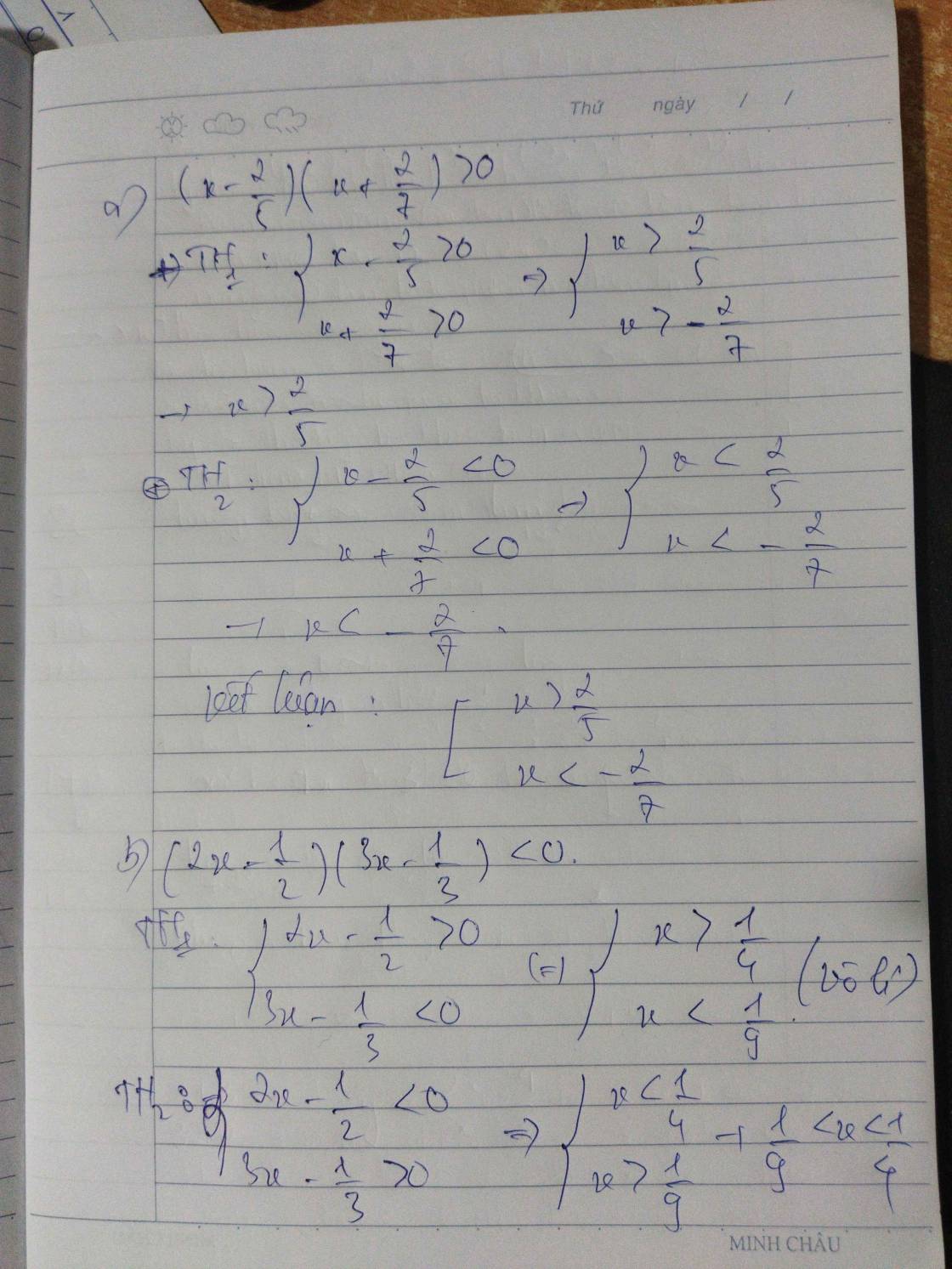
x + 2 = 0
{
x + 7 = 0
x = 2
{
x = 7
Vậy x = { 2 ; 7 }
k cho mình nhaaaa
<=> \(|x+2|=|x+7|\)
<=> \(\orbr{\begin{cases}x+2=x+7\\x+2=-x-7\end{cases}}\)
<=> \(\orbr{\begin{cases}0=5\\2x=-9\end{cases}}\)
<=> \(\orbr{\begin{cases}VL\\x=-\frac{9}{2}\end{cases}}\)
VẬY \(x=-\frac{9}{2}\)