Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\) => \(\frac{x^2}{4}=\frac{y^2}{9}=\frac{2z^2}{32}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x^2}{4}=\frac{y^2}{9}=\frac{2z^2}{32}=\frac{x^2+y^2-2z^2}{4+9-32}=\frac{76}{-19}=-4\)
=> \(\hept{\begin{cases}\frac{x^2}{4}=-4\\\frac{y^2}{9}=-4\\\frac{2z^2}{32}=-4\end{cases}}\) => \(\hept{\begin{cases}x^2=-4.4=-16\\y^2=-4.9=-36\\z^2=\left(-4.32\right):2=-64\end{cases}}\) => ko có giá trị x,y,z thõa mãn
Ta có: \(-2x=5y\) => \(\frac{x}{5}=\frac{y}{-2}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{5}=\frac{y}{-2}=\frac{x+y}{5-2}=\frac{30}{3}=10\)
=> \(\hept{\begin{cases}\frac{x}{5}=10\\\frac{y}{-2}=10\end{cases}}\) => \(\hept{\begin{cases}x=10.5=50\\y=10.\left(-2\right)=-20\end{cases}}\)
Vậy ..
\(\frac{x}{-3}=\frac{y}{-7}\Rightarrow\frac{2x}{-6}=\frac{4y}{-28}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{-6}=\frac{4y}{-28}=\frac{2x+4y}{(-6)+(-28)}=\frac{68}{-34}=-2\)
Vậy : \(\hept{\begin{cases}\frac{x}{-3}=-2\\\frac{y}{-7}=-2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=14\end{cases}}\)

Ta có:
\(\dfrac{x}{10}=\dfrac{y}{5}\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}\) (1)
\(\dfrac{y}{2}=\dfrac{z}{3}\Rightarrow\dfrac{y}{10}=\dfrac{z}{25}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{25}\)
Áp dụng tính chất dãy số bằng nhau ta có:
\(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{25}=\dfrac{2x-y+4z}{2\cdot20-10+4\cdot25}=\dfrac{270}{130}=\dfrac{27}{13}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{27}{13}\Rightarrow x=\dfrac{540}{13}\)
\(\Rightarrow\dfrac{y}{10}=\dfrac{27}{13}\Rightarrow y=\dfrac{270}{13}\)
\(\Rightarrow\dfrac{z}{25}=\dfrac{27}{13}=\dfrac{675}{13}\)
Có: \(\dfrac{x}{10}=\dfrac{y}{5}\Leftrightarrow\dfrac{x}{10}=\dfrac{2y}{10}\left(1\right)\)
\(\dfrac{y}{2}=\dfrac{z}{3}\Leftrightarrow\dfrac{2y}{10}=\dfrac{2z}{15}\left(2\right)\)
Từ (1) và (2) => \(\dfrac{x}{10}=\dfrac{2y}{10}=\dfrac{2z}{15}\)=> \(\dfrac{x}{10}=\dfrac{y}{5}=\dfrac{2z}{15}\)
Áp dung tính chất của dãy tỉ số bằng nhau và 2x - y + 4z = 270, ta có:
\(\dfrac{x}{10}=\dfrac{y}{5}=\dfrac{2z}{15}=\dfrac{2x}{20}=\dfrac{4z}{30}=\dfrac{2x-y+4z}{20-5+30}=\dfrac{270}{45}=6\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{10}=6\\\dfrac{y}{5}=6\\\dfrac{2z}{15}=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=60\\y=30\\z=45\end{matrix}\right.\)
Vậy...

a) |x - 1,7| = 2,3
Xét 2 trường hợp:
TH1: x - 1,7 = -2,3
x = -2,3 +1,7
x = -0,6
TH2: x - 1,7 = 2,3
x = 2,3 + 1,7
x = 4
Vậy: Tự kl :<
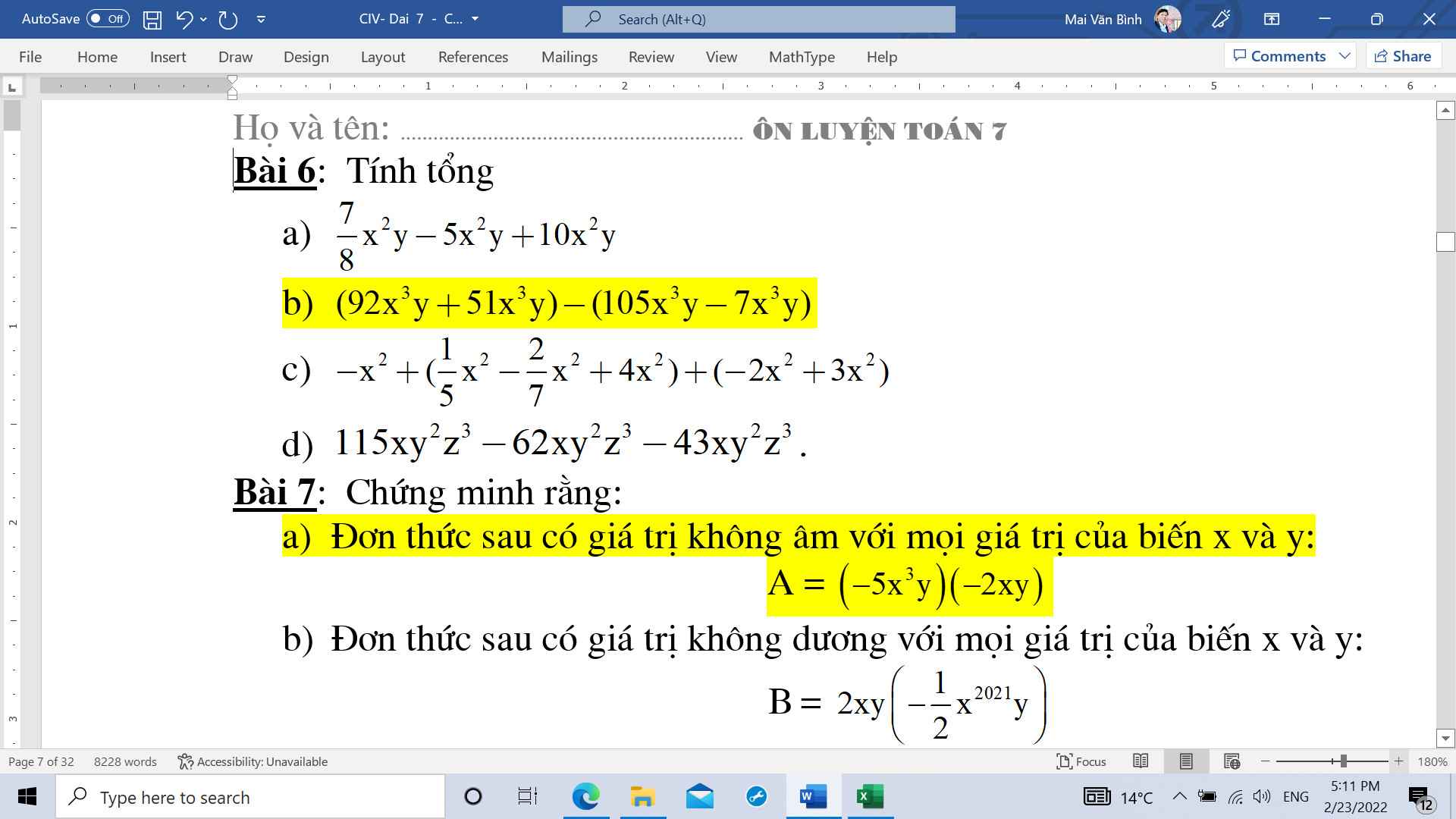
A = (\(x\) -1 )2 + |2\(x\) - y| + 2024
(\(\)\(x\) -1)2 ≥ 0 \(\forall\) \(x\); |2\(x\) - y| ≥ 0 ∀ \(x\)
⇒ (\(x\) - 1)2 + |2\(x\) - y| ≥ 2024
Amin = 2024 ⇔ \(\left\{{}\begin{matrix}x-1=0\\2x-y=2024\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x=1\\y=2x-2024\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x=1\\y=-2022\end{matrix}\right.\)
Vậy giá trị nhỏ nhất của biểu thức là: 2024 xảy ra khi \(\left\{{}\begin{matrix}x=1\\y=-2022\end{matrix}\right.\)
em cảm ơn ạ