
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2.\left(3+1\right).\left(3^2+1\right).\left(3^4+1\right)\)
= \(\left(6+2\right)\left(3^2+1\right)\left(3^4+1\right)\)
= \(\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\)
= \(\left(3^4-1\right)\left(3^4+1\right)\)
= \(3^8-1\)
Chúc bạn học tốt !!!

Bài làm:
Ta có: \(\left(x+3\right)^2-9\left(y-3\right)^2\)
\(=\left(x+3\right)^2-\left[3\left(y-3\right)\right]^2\)
\(=\left[x+3-3\left(y-3\right)\right]\left[x+3+3\left(y-3\right)\right]\)
\(=\left(x+3-3y+9\right)\left(x+3+3y-9\right)\)
\(=\left(x-3y+12\right)\left(x+3y-6\right)\)
\(\left(x+3\right)^2-9\left(y-3\right)^2\)
\(=\left[x+3+3\left(x-3\right)\right].\left[x+3-3\left(x-3\right)\right]\)

c) \(\left(x^2-y^2\right)^2=x^4-2x^2y^2+y^4\)
c) \(\left(x^2+3^2\right)^2=x^4+18x+81\)
c) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)
c) \(\left(3x-y^2\right)^2=9x^2-6xy^2+y^4\)
c) \(\left(x+2y^2\right)^2=x^2+4xy^2+4y^4\)
c) \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)
c) \(\left(2x+3y^2\right)^2=4x^2+12xy^2+9y^4\)
c) \(\left(4x-2y^2\right)^2=16x^2-16xy^2+4y^4\)
c) \(\left(4x^2-2y\right)^2=16x^4-16x^2y+4y^2\)
c) \(\left(\dfrac{1}{x}-5\right)\left(\dfrac{1}{x}+5\right)=\dfrac{1}{x^2}-25\)
c) \(\left(x-\dfrac{3}{2}\right)\left(x+\dfrac{3}{2}\right)=x^2-\dfrac{9}{4}\)
c) \(\left(\dfrac{x}{3}-\dfrac{y}{4}\right)\left(\dfrac{x}{3}+\dfrac{y}{4}\right)=\dfrac{x^2}{9}-\dfrac{y^2}{16}\)
c) \(\left(\dfrac{x}{y}-\dfrac{2}{3}\right)\left(\dfrac{x}{y}+\dfrac{2}{3}\right)=\dfrac{x^2}{y^2}-\dfrac{4}{9}\)
c) \(\left(\dfrac{x}{2}+\dfrac{y}{3}\right)\left(\dfrac{y}{3}-\dfrac{x}{2}\right)=\dfrac{y^2}{9}-\dfrac{x^2}{4}\)
c) \(\left(2x-\dfrac{2}{3}\right)\left(\dfrac{2}{3}+2x\right)=4x^2-\dfrac{4}{9}\)
c) \(\left(2x+\dfrac{3}{5}\right)\left(\dfrac{3}{5}-2x\right)=\dfrac{9}{25}-4x^2\)
c) \(\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{4}{4}+\dfrac{1}{2}x\right)=\dfrac{1}{4}x^2-\dfrac{16}{9}\)
c) \(\left(\dfrac{2}{3}x^2-\dfrac{y}{2}\right)\left(\dfrac{2}{3}x^2+\dfrac{y}{2}\right)=\dfrac{4}{9}x^4-\dfrac{y^2}{4}\)


a) (x + 3)2 - 2(x + 3)(x - 2) + (x - 2)2
= (x + 3 - x + 2)2 = 52 = 25
b) (2x + 5)2 + 2(2x + 5)(3x - 1) + (3x - 1)2
= (2x + 5 + 3x - 1)2 = (5x + 4)2

\(64x^3y^3-11=\left(4xy\right)^3-\left(\sqrt[3]{11}\right)^3\)
\(\left(4xy-\sqrt[3]{11}\right)\left(16x^2y^2+4\sqrt[3]{11}xy+\sqrt[3]{11^2}\right)\)

( 2x - 3y )2 = 4x2 - 12xy + 9y2
( 3√x - y )2 = 9x - 6y√x + y2 ( x ≥ 0 )

\(a)\)
\(4x^2-4x+1\)\(=\left(2x-1\right)^2\)
\(b)\)
\(\left(3x+2\right)\left(2-3x\right)\)\(=4-9x^2\)
\(c)\)
\(\left(x-3\right)\left(x^2+3x+9\right)\)\(=x^3-27\)
\(a,4x^2-4x+1=\left(2x\right)^2-2.2x.1+1=\left(2x-1\right)^2\)
\(b,\left(3x+2\right)\left(2-3x\right)=\left(2+3x\right)\left(2-3x\right)=2^2-\left(3x\right)^2\)
\(c,\left(x-3\right)\left(x^2+3x+9\right)=\left(x-3\right)\left(x^2+3x.1+3^2\right)=x^3-3^3\)
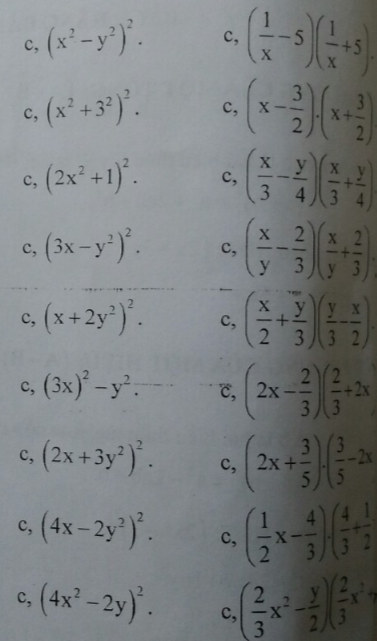 viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp
viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp
Đặt 1+x4y4+2x2y2 =A
4A=4+4x4y4+8xxy2
=(2x2y2+2)2
A=\(\frac{\left(\text{2x^2y^2+2 }\right)^2}{4}\)
Ta có : x4y4 + 2x2y2 + 1
= ( x2y2 + 1 )2