B
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
22 tháng 6 2017
2,131131131...
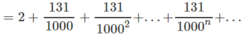
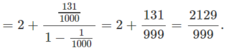
(Vì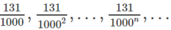 
là một cấp số nhân lùi vô hạn với công bội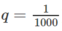 
)
CM
24 tháng 3 2017
Ta có: a= 1,02020202... ( chu kì 2)
= 1 + 0,02+ 0,0002+ 0,000002 + .....
Là tổng của cấp số nhân lùi vô hạn có số hạng đầu là
SG
1
,...,131/
10 tháng 4 2017
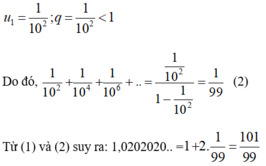
\(a=34,\left(12\right)\)
\(=34\dfrac{12}{99}=34\dfrac{4}{33}=\dfrac{1126}{33}\)
TK
2
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2021
Xét tổng vô hạn:
\(S_n=0,2+0,07+0,007+0,0007+...\)
\(S_n=\dfrac{1}{5}+\dfrac{7}{100}+\dfrac{7}{1000}+\dfrac{7}{10000}+...\)
\(S_n=\dfrac{1}{5}+\dfrac{7}{100}\left(1+\dfrac{1}{10}+\dfrac{1}{10^2}+...\right)\)
\(S_n=\dfrac{1}{5}+\dfrac{7}{100}.\dfrac{1}{1-\dfrac{1}{10}}=\dfrac{5}{18}\)
Vậy \(0,277777...=\dfrac{5}{18}\)
TP
9 tháng 3 2021
Xét tổng vô hạn:
Sn=0,2+0,07+0,007+0,0007+...Sn=0,2+0,07+0,007+0,0007+...
Sn=15+7100+71000+710000+...Sn=15+7100+71000+710000+...
Sn=15+7100(1+110+1102+...)Sn=15+7100(1+110+1102+...)
Sn=15+7100.11−110=518Sn=15+7100.11−110=518
Vậy 0,277777...=518
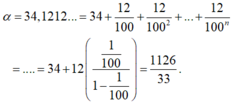
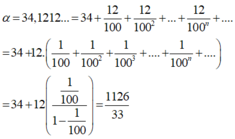
\(0,444... = 0,4 + 0,04 + 0,004 + ...\)
Số \(0,444...\) là tổng của cấp số nhân lùi vô hạn có số hạng đầu bằng \(0,4\) và công bội bằng \(\frac{1}{{10}}\).
Do đó: \(0,444... = \frac{{0,4}}{{1 - \frac{1}{{10}}}} = \frac{4}{9}\)