Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(y'=\frac{x^2-2x}{\left(x-1\right)^2}\)
Gọi \(M\left(x_0;y_0\right)\) là tọa độ tiếp điểm của tiếp tuyến d với (C)
\(d:y=\frac{x_0^2-2_0x}{\left(x_0-1\right)^2}\left(x-x_0\right)+\frac{x_0^2-x_0+1}{x_0-1}\)
a) Vì d song song với đường thẳng \(\Delta:y=\frac{3}{4}x+\frac{1}{4}\) nên ta có :
\(\frac{x_0^2-2_0x}{\left(x_0-1\right)^2}=\frac{3}{4}\Leftrightarrow x_0^2-2_0x-3=0\Leftrightarrow x_0=-1;x_0=3\)
* \(x_0=-1\) phương trình tiếp tuyến : \(y=\frac{3}{4}x-\frac{3}{4}\)
* \(x_0=3\) phương trình tiếp tuyến : \(y=\frac{3}{4}x+\frac{5}{4}\)
b) Đường thẳng \(\Delta_m\) có hệ số góc \(k_m=\frac{1}{m}\)
Số tiếp tuyến thỏa mãn bài toán chính là số nghiệm của phương trình :
\(y'.k_m=-1\Leftrightarrow\frac{m\left(x^2-2x\right)}{\left(x-1\right)^2}=-1\)
\(\Leftrightarrow\left(m+1\right)x^2-2\left(m+1\right)x+1=0\left(1\right)\)
* Nếu m = - 1 suy ra (1) vô nghiệm, suy ra không có tiếp tuyến nào
* Nếu \(m\ne-1\), suy ra (1) có \(\Delta'=m\left(m+1\right)\) và (1) có nghiệm \(x=1\Leftrightarrow m=0\)
+ Khi \(\left[\begin{array}{nghiempt}m>0\\m< -1\end{array}\right.\) suy ra (*) có 2 nghiệm phân biệt nên có 2 tiếp tuyến
+ Khi \(-1< m\le0\) thì (*) vô nghiệm nên không có tiếp tuyến nào

Gọi \(M\left(x_0;y_0\right)\)là tiếp điểm. Ta có : \(y'=-3x^2+3\)
a) Vì tiếp tuyến vuông góc với đường thẳng \(x+y-1=0\Rightarrow y=-x+1\) nên ta có :
\(y'\left(x_0\right)=1\Leftrightarrow-3x^2_0+3=1\Leftrightarrow x_0=\pm\frac{\sqrt{6}}{3}\)
* \(x_0=\frac{\sqrt{6}}{3}\Rightarrow y_0=\frac{18+7\sqrt{6}}{9}\) nên ta có phương trình tiếp tuyến
\(y=\left(x-\frac{\sqrt{6}}{3}\right)+\frac{18+7\sqrt{6}}{9}=x+\frac{18+7\sqrt{6}}{9}\)
* \(x_0=-\frac{\sqrt{6}}{3}\Rightarrow y_0=\frac{18-7\sqrt{6}}{9}\) nên ta có phương trình tiếp tuyến
\(y=\left(x+\frac{\sqrt{6}}{3}\right)+\frac{18-7\sqrt{6}}{9}=x+\frac{18-7\sqrt{6}}{9}\)
b) Ta có \(y'=-3x^2_0+3\le3\) với mọi \(x_0\Rightarrow maxy'=3\) đạt được khi \(x_0=0\)Tiếp tuyến có hệ số góc nhỏ nhất có tiếp điểm là \(M\left(0;2\right)\) và \(y'\left(x_0\right)=3\) nên ta có phương trình : \(y=3x+2\) c) Gọi hệ số góc của tiếp tuyến là k thì \(\overrightarrow{n}\left(k;-1\right)\) là vectơ pháp tuyến của \(\Delta\)Vì \(\Delta\) tạo với \(\Delta'\) một góc bằng \(45^0\) nên \(\frac{\left|k-1\right|}{\sqrt{k^2+1}.\sqrt{2}}=\frac{\sqrt{2}}{2}\Leftrightarrow k=0\)
Ta có \(f'\left(x_0\right)=k\Leftrightarrow-3x^2_0+3=0\Leftrightarrow x_0=\pm1\)
* \(x_0=1\Rightarrow y_0=4\Rightarrow\Delta:y-4=0\)
* \(x_0=-1\Rightarrow y_0=-2\Rightarrow\Delta:y+2=0\)

a)
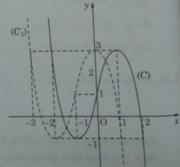
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
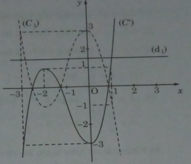
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
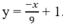
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 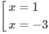
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.

Ta có: y′ = –4 x 3 – 2x
Vì tiếp tuyến vuông góc với đường thẳng y = x/6 – 1 nên tiếp tuyến có hệ số góc là –6. Vì vậy:
–4 x 3 – 2x = –6
⇔ 2 x 3 + x – 3 = 0
⇔ 2( x 3 – 1) + (x – 1) = 0
⇔ (x – 1)(2 x 2 + 2x + 3) = 0
⇔ x = 1(2 x 2 + 2x + 3 > 0, ∀ x)
Ta có: y(1) = 4
Phương trình phải tìm là: y – 4 = -6(x – 1) ⇔ y = -6x + 10

a) Học sinh tự làm
b) Ta có: y′ = –4 x 3 – 2x
Vì tiếp tuyến vuông góc với đường thẳng y = x/6 – 1 nên tiếp tuyến có hệ số góc là –6. Vì vậy:
–4 x 3 – 2x = –6
⇔ 2 x 3 + x – 3 = 0
⇔ 2( x 3 – 1) + (x – 1) = 0
⇔ (x – 1)(2 x 2 + 2x + 3) = 0
⇔ x = 1(2 x 2 + 2x + 3 > 0, ∀x)
Ta có: y(1) = 4
Phương trình phải tìm là: y – 4 = -6(x – 1) ⇔ y = -6x + 10

Gọi \(M\left(x_0;2x^3_0+3x^2_0-12x_0-1\right)\) là tiếp điểm
\(\Delta:y=\left(6x^2_0+6x_0-12\right)\left(x-x_0\right)+2x^3_0+3x^2_0-12x_0-1\)
Vì \(O\in\Delta\) nên \(0=\left(6x^2_0+6x_0-12\right)\left(-x_0\right)+2x^3_0+3x^2_0-12x_0-1\)
\(\Leftrightarrow4x^3_0+3x^2_0+1\Leftrightarrow x_0=-1\Rightarrow y_0=12;y'\left(x_0\right)=-12\)
Vậy \(\Delta:y=-12x\)
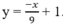

Gọi hệ số góc của \(\Delta\) là k \(\Rightarrow\overrightarrow{n_{\Delta}}=\left(k;-1\right);\overrightarrow{n_d}=\left(3;1\right)\)
Yêu cầu bài toán :
\(\Leftrightarrow\frac{\left|3k-1\right|}{\sqrt{1+k^2}.\sqrt{10}}=\frac{1}{\sqrt{2}}\)
\(\Leftrightarrow2k^2-3k-2=0\)
\(\Leftrightarrow k=-\frac{1}{2}\) hoặc k = 2
Từ đó ta có được 2 tiếp tuyến là \(y=2x-2;y=2x-\frac{22}{27}\)