NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 11 2017
giúp em bài này với ạ :
tìm x biết :
\(\sqrt{x-1}=5\) \(;\sqrt{\left(x-\frac{1}{3}\right)^2=7}\) \(;\sqrt{1+x}+5=3\)
AA
Admin (a@olm.vn)
Admin
VIP
27 tháng 8 2015
Qua các câu trả lời của Thầy Giáo Toán, Admin tin rằng bạn là Thầy giáo đích thực. Cảm ơn Thầy Giáo Toán rất nhiều vì đã giúp cho các thành viên trên Online Math. Mong được có dịp gặp mặt Thầy.
TG
1
29 tháng 1
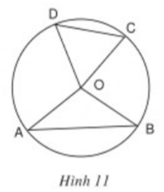
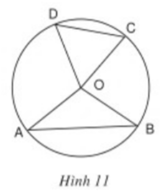
a: Xét (O) có AB là đường kính
nên \(sđ\stackrel\frown{AB}=180^0\)
\(sđ\stackrel\frown{DA}_{nhỏ}=sđ\stackrel\frown{AC}_{nhỏ}+sđ\stackrel\frown{CD}_{nhỏ}\)
\(=60^0+60^0=120^0\)
\(sđ\stackrel\frown{DA}_{lớn}=360^0-sđ\stackrel\frown{DA}_{nhỏ}=360^0-120^0=240^0\)
b:
\(sđ\stackrel\frown{CB}=sđ\stackrel\frown{CD}+sđ\stackrel\frown{BD}=60^0+60^0=120^0\)
Xét (O) có
\(\widehat{TCB}\) là góc tạo bởi tiếp tuyến CT và dây cung CB
=>\(\widehat{TCB}=\dfrac{1}{2}\cdot sđ\stackrel\frown{CB}=\dfrac{1}{2}\cdot120^0=60^0\)
Xét (O) có
\(\widehat{TCD}\) là góc tạo bởi tiếp tuyến CT và dây cung CD
=>\(\widehat{TCD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{CD}=\dfrac{1}{2}\cdot60^0=30^0\)
=>\(\widehat{TCD}=\dfrac{1}{2}\cdot\widehat{TCB}\)
=>CD là phân giác của góc BCT
a: Xét tứ giác MAOC có
góc MAO+góc MCO=180 độ
nên MAOC là tứ giác nội tiếp
b: Xét (O) có
MA,MC là tiếp tuyến
nên MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc với AC tại trung điểm của AC
Xét ΔABC có AO/AB=AI/AC
nên OI//BC và BC=2OI
Xét ΔACF và ΔADF có
AC=AD
góc CAF=góc DAF
AF chung
Do đó: ΔACF=ΔADF
=>góc ADF=90 độ
=>DF làtiếp tuyến của (O;R)