
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a^n:a^m=a^{n-m}\)
\(a^n\cdot a^m=a^{n+m}\)
\(\left(a^n\right)^m=a^{n\cdot m}\)
\(\left(a\cdot b\right)^n=a^n\cdot b^n\)
\(\left(\dfrac{a}{b}\right)^n=\dfrac{a^n}{b^n}\)



\(\left(\dfrac{1}{7}\right)^7\cdot7^7\)
\(=\left(\dfrac{1}{7}\cdot7\right)^7\)
\(=\left(\dfrac{7}{7}\right)^7\)
\(=1^7\)
\(=1\)
_______
\(\dfrac{3^7}{\left(0,375\right)^7}\)
\(=\left(\dfrac{3}{0,375}\right)^7\)
\(=8^7\)
\(=\left(2^3\right)^7\)
\(=2^{21}\)

a) 272 : 253
= (33)2 : (52)3
= 36 : 56
\(=\left(\frac{3}{5}\right)^6\)
b) 254 : 28
= (52)4 : 28
= 58 : 28
\(=\left(\frac{5}{2}\right)^8\)

Công thức chung :
a, Phép cộng : \(\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m}\)
b, Phép trừ : \(\frac{a}{m}-\frac{b}{m}=\frac{a}{m}+\left(\frac{-b}{m}\right)\)
c, Phép nhân : \(\frac{a}{b}\cdot\frac{c}{d}=\frac{ac}{bd}\)
d, Phép chia : \(\frac{a}{b}:\frac{c}{d}=\frac{ad}{bc}\)
đ, Phép luỹ thừa :
1, Nhân 2 luỹ thừa cùng cơ số : \(\left(\frac{a}{b}\right)^m.\left(\frac{a}{b}\right)^n=\left(\frac{a}{b}\right)^{m+n}\)
2, Chia 2 luỹ thừa cùng cơ số : \(\left(\frac{a}{b}\right)^m:\left(\frac{a}{b}\right)^n=\left(\frac{a}{b}\right)^{m-n}\left(\frac{a}{b}\ne0,m\ge n\right)\)
3, Luỹ thừa của luỹ thừa : \([\left(\frac{a}{b}\right)^m]^{^n}=\left(\frac{a}{b}\right)^{m.n}\)
4. Luỹ thừa có số mũ là 1 luỹ thừa : \(\left(\frac{a}{b}\right)^{m^n}\), ta tính \(m^n\) trước, rồi tính luỹ thừa \(\frac{a}{b}\) với số đó.
Chúc học tốt !

a) \(7^5:343\)
\(=7^5:7^3\)
\(=7^{5-3}\)
\(=7^2\)
b) \(a^{12}:a^{18}\)
\(=\dfrac{a^{12}}{a^{18}}\)
\(=\dfrac{a^0}{a^6}\)
\(=\dfrac{1}{a^6}\)
c) \(x^7\cdot x^4\cdot x\)
\(=x^{7+4+1}\)
\(=x^{12}\)

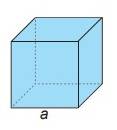
Công thức tính thể tích hình lập phương cạnh a là:
V= a.a.a = \({a^3}\)
Bài toán mở đầu:
Biểu thức lũy thừa tính toàn bộ lượng nước trên Trái Đất trong bài toán mở đầu (đơn vị kilomét khối) là:
V =\({(1111,34)^3}\)

a) Ta có: \(P\left(x\right)=2+5x^2-3x^3+4x^2-2x-x^3+6x^5\)
\(=6x^5-\left(3x^3+x^3\right)+\left(5x^2+4x^2\right)-2x+2\)
\(=6x^5-4x^3+9x^2-2x+2\)
Tham khảo
Lũy thừa của một số hữu tỉ - Các phương pháp giải toán 7 | Hoc360.net
\(a^m\cdot a^n=a^{m+n}\)