K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
0
T
0
vẽ hình hộ thôi ạ
vẽ hộ hình mik vs ạ, cám ơn!!
vẽ hộ mình hình với mn ơi mình ko có thước vẽ ức chế vl
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
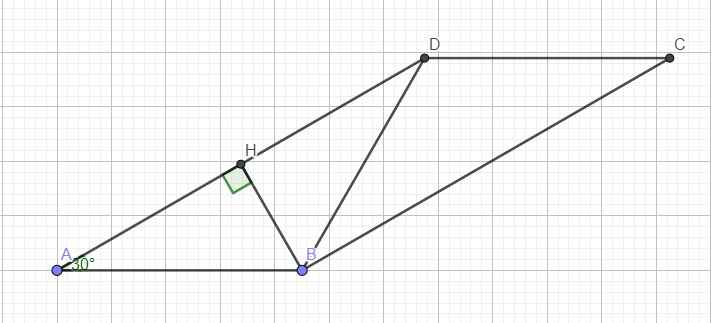
Kẻ đường cao BH ứng với AD
Do \(AB=AD\Rightarrow\Delta ABD\) cân tại B
\(\Rightarrow\) BH là đường cao đồng thời là trung tuyến
\(\Rightarrow AH=HD=\dfrac{1}{2}AD\)
Trong tam giác vuông ABH ta có:
\(sinA=\dfrac{BH}{AB}\Rightarrow BH=AB.sinA=18.sin30^0=9\left(cm\right)\)
\(cosA=\dfrac{AH}{AB}\Rightarrow AH=AB.cosA=18.cos30^0=9\sqrt{3}\left(cm\right)\)
\(\Rightarrow AD=2AH=18\sqrt{3}\left(cm\right)\)
\(S_{ABCD}=BH.AD=162\sqrt{3}\left(cm^2\right)\)
30 tháng 3 2021
Câu IV:
1) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay B,F,E,C cùng nằm trên 1 đường tròn(đpcm)
T
4 tháng 3 2021
Mình làm dựa vào những gì đề đã có nhé. Câu nào đề thiếu mình sẽ không giải.
1. Kẻ đường kính AK của đường tròn (O). Do A là điểm chính giữa cung BC nên OA là đường trung trực BC. Mặt khác I là trung điểm BC nên O, A, I thẳng hàng \(\Rightarrow\angle BIA=90^o.\)
Do AK là đường kính đường tròn (O) nên \(\angle ABK=90^o\Rightarrow AB^2=AI\cdot AK.\) (hệ thức lượng)
Xét $\Delta AID$ và $\Delta AEK$ có
$\angle A:$ chung
$\angle AID =\angle AEK=90^o$
\(\Rightarrow\Delta AID\sim\Delta AEK\Rightarrow\dfrac{AI}{AE}=\dfrac{AD}{AK}\Rightarrow AD\cdot AE=AI\cdot AK=AB^2\) (đpcm)
2. Xét tứ giác AHIC có
\(\angle AHC=\angle AIC=90^o\Rightarrow\) AHIC là tứ giác nội tiếp \(\Rightarrow\) A, I, C, H đồng viên (đpcm).
3. Chưa đủ dữ kiện để giải.