
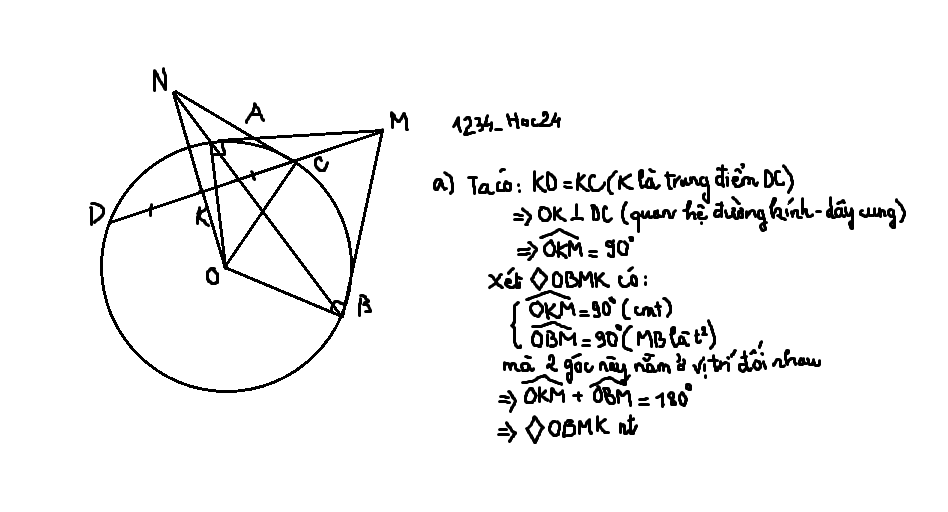
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

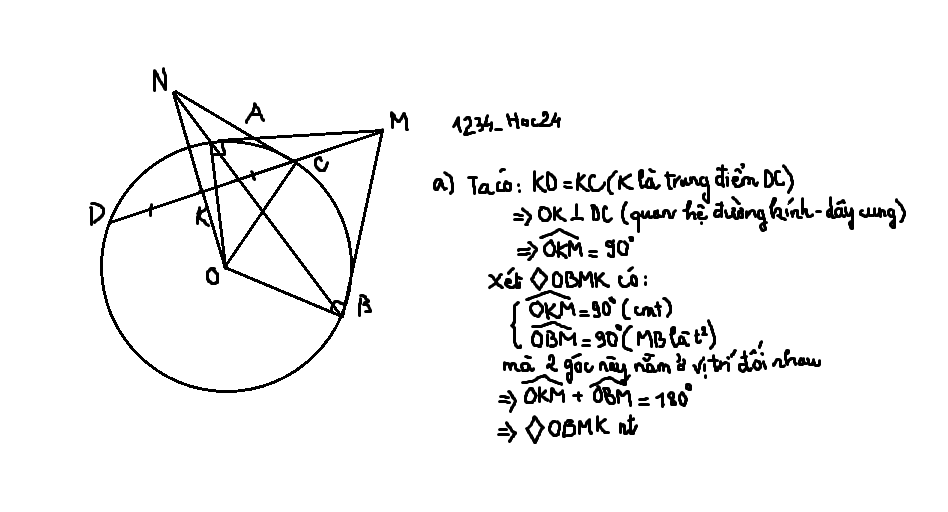

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

Mình bổ sung thêm ạ, sau khi xét xong tứ giác và suy ra cộng bằng 180 : Mà 2 góc này ở vị trí đối nhau ạ

a. Vì \(\widehat{AMB}=90^0\) (góc nt chắn nửa đg tròn) nên AMB vuông tại M
Áp dụng HTL: \(BM.BC=AB^2=\left(2R\right)^2=4R^2\)
b. Vì AMBD nội tiếp (O) nên \(\widehat{MAB}=\widehat{HDB}\) (cùng chắn MB)
Vì \(\widehat{MAH}=\widehat{HDB};\widehat{MHA}=\widehat{BHD}=90^0\) nên \(\Delta MAH\sim\Delta BDH\left(g.g\right)\)
\(\Rightarrow\dfrac{HM}{HB}=\dfrac{HA}{HD}\Rightarrow MD.HD=HA.HB\)


a: Xét tứ giác MAOB có \(\widehat{OAM}+\widehat{OBM}=180^0\)
nên MAOB là tứ giác nội tiếp
Xét ΔMBD và ΔMCB có
\(\widehat{MBD}=\widehat{MCB}\)
\(\widehat{BMD}\) chung
Do đó: ΔMBD\(\sim\)ΔMCB
Suy ra: MB/MC=MD/MB
hay \(MB^2=MC\cdot MD\left(1\right)\)
b: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
mà OA=OB
nên OM là đường trung trực của AB
Xét ΔOBM vuông tại B có BH là đườg cao
nên \(MH\cdot MO=MB^2\left(2\right)\)
Từ (1) và (2) suy ra \(MD\cdot MC=MH\cdot MO\)

Vì \(\widehat{BEC}=\widehat{BKC}=90^0\)(góc nt chắn nửa đg tròn) nên \(HK\perp MC;ME\perp HC\)
Xét tam giác HMC có 2 đường cao HK,ME (cm trên) cắt nhau tại B nên B là trực tâm
Do đó BC⊥MH