
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn đợi mình tí ha hình vẽ ko up lên bình luận được nên tí mình up lên trang cá nhân bạn vô bạn xem ha
a, ta có: AB, AC là 2 tiếp tuyến của (O); OC=OB (=R); AB=AC (t/chat 2 tiếp tuyến cắt nhau)
=>OE là đường trung trực của BC =>OE ⊥ BC
Xét (O) có: OA=OB=OC=R=AB/2 =>△ABC vuông tại C
b, ta có: AD=DC (t/chat 2 tiếp tuyến cắt nhau)
BE=CE (t/chat 2 tiếp tuyến cắt nhau)
Mà DC+CE=DE => DE=AD+BE
c, gọi I là giao điểm của OD và AC; K là giao điểm của BC và OE
Xét tứ giác OICK có:
∠OIC = ∠ICK = ∠OKC (=90*)
=> OICK là hình chữ nhật => ∠IOK=90* hay ∠DOE=90*
d, ta có: ∠AOD=∠COD (t/chat 2 tiếp tuyến cắt nhau)
∠COE=∠BOE (t/chat 2 tiếp tuyến cắt nhau)
Mà ∠DOC+∠COE=∠DOE=90* =>∠AOD+∠BOE=90*
Xét △ADO và △BEO có:
∠DAO=∠OBE (=90*); ∠ADO=∠BOE (cùng phụ với ∠AOD)
=>△ADO đồng dạng △BEO =>AD/BE=AO/BO.....
Hình như đề sai hay sao á làm ko ra câu d bạn ơi

1, Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\end{matrix}\right.\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}\approx90^0-53^0=37^0\)
2,
a, Áp dụng HTL: \(\left\{{}\begin{matrix}AD\cdot AB=AH^2\\AE\cdot AC=AH^2\end{matrix}\right.\Rightarrow AD\cdot AB=AE\cdot AC\)
b, \(AD\cdot AB=AE\cdot AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\Rightarrow\Delta ABC\sim\Delta AED\left(c.g.c\right)\)



Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

 vẽ hình giúp mình luôn
vẽ hình giúp mình luôn



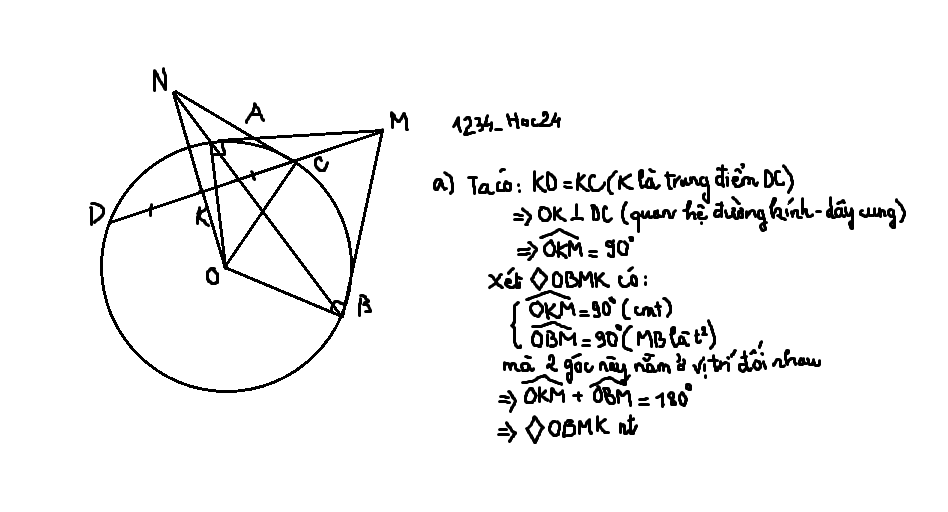
Mình bổ sung thêm ạ, sau khi xét xong tứ giác và suy ra cộng bằng 180 : Mà 2 góc này ở vị trí đối nhau ạ