Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp: Sử dụng phương pháp tọa độ trong mặt phẳng.
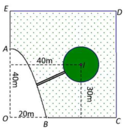
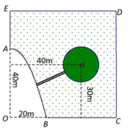
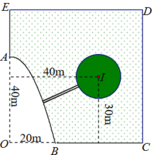
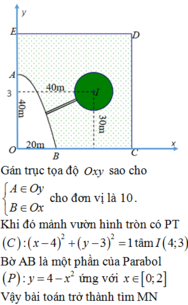
Cách giải: Chọn hệ trục tọa độ Đề các vuông góc như sau:
Gốc O, chiều dương trục hoành là tia OC, chiều dương trục tung là tia OE, đơn vị hai trục là đơn vị độ dài 1m
Khi đó ta có phương trình Parabol là

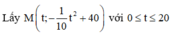
nằm trên Parabol thì khoảng cách ngắn nhất từ đường tròn đến M là
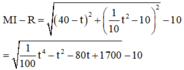
Khảo sát hàm số suy ra khoảng cách ngắn nhất xấp xỉ 17,7

C/m 3 điểm thẳng hàng là tìm trọng tâm của tam giác đóa pạn, có trọng tâm ròi =>D,M.F thẳng hàng


hình như trên
+)Ta có: ( g-c-g) ( Vì cùng bằng )
Nên MD = NE.
+)Xét và :
( Hai góc đối đỉnh)
Nên ( cgv - gn)
+)Từ B và C kẻ các đường thẳng lần lượt vuông
Góc với AB và AC cắt nhau tại J.
Ta có:
Nên J thuộc AL đường trung trực ứng với BC
Mặt khác : Từ ( Câu a)
Ta có : BM = CN
BJ = CJ ( cm trên)
Nên ( c-g-c)
hay đường trung trực của MN
Luôn đi qua điểm J cố định.

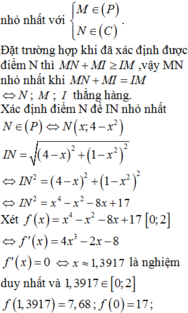

( Hình thì bạn tự vẽ )
a/ ta có góc xOy là góc nhọn
=> xOy < 90độ
=> MOx= MOy<45 độ (1) .
Mặt khác: Giả sử OA>MA
=> AMO > MOA <=> 180 - BMO>MOA
<=> 180 - (MOA + OAM)> MOA
<=> 180 -(MOA+90)>MOA
<=> 90>2MOA
<=>MOA<45
<=> MOx<45 (đúng do (1))
Vậy OA>MA
b/ Giả sử OB>OM .
Khi đó: OMB > OBM
<=> OMB>180 - OMB - MOB
<=> 2OMB>180-MOA
<=>2OMB>180-(90-OMA)
<=> 2OMB-OMA>90
<=> 2OMB-(180-OMB)>90
<=> 3OMB>270
<=> OMB>90 (đúng do OMB= OAM + AOM=90+AOM)
Vậy OB >OM
vẽ hình hộ tui