Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc MAO+góc MBO=90+90=180 độ
=>MAOB nội tiếp
ΔOCD cân tại O
mà OK là trung tuýen
nên OK vuông góc CD
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
góc OHE+góc OKE=90+90=180 độ
=>OHEK nội tiếp
b: Xét ΔMAE và ΔMKA có
góc MAE=góc MKA
góc AME chung
=>ΔMAE đồng dạng với ΔMKA
=>MA/MK=ME/MA
=>MA^2=MK*ME=MC*MD

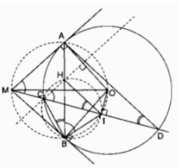

A, B, I nhìn MO cố định dưới một góc bằng 90° nên A, B, I nằm trên đường tròn bán kính MO.
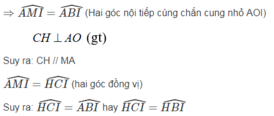
B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.


MC*MD=MH*MO
=>ΔMHC đồng dạng với ΔMDO
=>OHCD nội tiếp
=>góc OHD=góc OCD
=>góc OHD=góc MHC
GỌi K là giao của AB và CD
=>90 độ-góc OHD=90 độ-góc MHC
=>góc DHK=góc KHC
=>HK là phân giác của góc PHC
Vì NM vuông góc HK
nên HM là phân giác góc ngoài của góc PHC
=>MC/MD=HC/HD; CK/DK=HC/HD
=>MC/MD=CK/DK
CP//AD
=>CP/AD=MC/MD
CQ//AD
=>CQ/AD=CK/DK
=>CP/AD=CQ/AD
=>CP=CQ
=>ĐPCM

MC*MD=MH*MO
=>MC/MO=MH/MD
=>ΔMCH đồng dạng với ΔMOD
=>goc MHC=góc MDO=góc ODC
=>OHCD nội tiếp
=>góc OHD=góc OCD
ΔOCD cân tại O nên góc ODC=góc OCD
=>góc OHD=góc MHC
=>90 dộ-góc OHD=90 độ-góc MHC(1)
Gọi K là giao của AB và CD
(1)=>góc DHK=góc KHC
=>HK là phân giác trong của góc DHC
Vì HM vuông góc HK
nên HM là phân giác góc ngoài của ΔDHC
MC/MD=HC/HD=CK/DK
CP//AD
=>CP/AD=MC/MD
CQ//AD
=>CQ/AD=CK/DK
Từ (3), (4), (5) suy ra CP/AD=CQ/AD
=>CP=CQ
=>C là trung điểm của PQ

a) tứ giác AOBM nội tiếp thì có tâm đường tròn là trung điểm OM
cần CM tứ giác OIMB nội tiếp: dùng tổng hai góc đối cộng với nhau bằng 180o, mà đã có OBM=90o, mà I là trung điểm dây cung CD nên OI vuông góc CD luôn => OIM=90o
Vậy tứ giác OIMB nội tiếp thì tâm đường tròn cũng tại trung điểm OM luôn
b) 5 điểm A,I,O,B,M cùng thuộc 1 đtron
=> tứ giác AIOB nội tiếp => góc AIB=AOB (cùng chắn cung)
tứ giác AIOM nội tiếp => góc AIM=AOM (ccc)
mà góc AOM=1/2AOB=AIM=1/2AIB
=> BIM=1/2AIB (đpcm