QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Tập giá trị của hàm số \(y = \tan x\) là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Như vậy, hàm số \(y = \tan x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)
Như vậy, hàm số \(y = \tan x\) có tuần hoàn
d) Hàm số \(y = \tan x\)đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\) với \(k \in Z\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Hàm số nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\), thì \(y < 0\) khi \(x\; \in \left( { - \frac{\pi }{2};0} \right) \cup \left( {\frac{\pi }{2};\;\pi } \right)\)
PT
1
CM
6 tháng 4 2017
Đồ thị hàm số y = sin x:
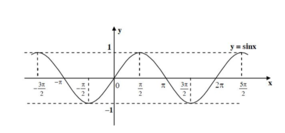
Dựa vào đồ thị hàm số y = sin x ta thấy
y = sin x > 0
⇔ x ∈ (-2π; -π) ∪ (0; π) ∪ (2π; 3π) ∪…
hay x ∈ (k2π; π + k2π) với k ∈ Z.
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 là \(\left( {2; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \({2^x} > 4\) là \(\left( {2; + \infty } \right)\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2021
\(y'=\dfrac{3}{\left(x+1\right)^2}\Rightarrow\) phương trình tiếp tuyến tại \(M\left(m;\dfrac{m-2}{m+1}\right)\) có dạng:
\(y=\dfrac{3}{\left(m+1\right)^2}\left(x-m\right)+\dfrac{m-2}{m+1}\)
\(\Leftrightarrow3x-\left(m+1\right)^2y+m^2-4m-2=0\)
\(P=d\left(I;d\right)=\dfrac{\left|6m+6\right|}{\sqrt{9+\left(m+1\right)^4}}=\dfrac{6}{\sqrt{\left(m+1\right)^2+\dfrac{9}{\left(m+1\right)^2}}}\le\dfrac{6}{\sqrt{2\sqrt{\dfrac{9\left(m+1\right)^2}{\left(m+1\right)^2}}}}=\sqrt{6}\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left(m+1\right)^2=\dfrac{9}{\left(m+1\right)^2}\Leftrightarrow\left(m+1\right)^2=3\Rightarrow m=\) ... lại xấu :)
CM
15 tháng 7 2019
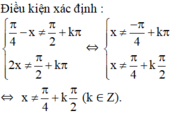
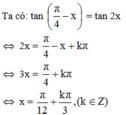
Kết hợp với điều kiện xác định suy ra
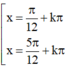(k ∈ Z)
Vậy với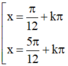 
(k ∈ Z)
thì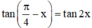 
31 tháng 10 2023
a: Đường thẳng y=1 cắt đồ thị y=tanx tại một điểm duy nhất là \(\left(\dfrac{\Omega}{4};1\right)\)
b: \(tanx=1\)
=>\(x=\dfrac{\Omega}{4}+k\Omega\left(k\in Z\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2021
\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi tiếp tuyến d qua A có dạng: \(y=k\left(x-m\right)+1\)
d là tiếp tuyến của (C) khi hệ sau có nghiệm: \(\left\{{}\begin{matrix}\dfrac{2-x}{x-1}=k\left(x-m\right)+1\\\dfrac{-1}{\left(x-1\right)^2}=k\end{matrix}\right.\)
\(\Rightarrow\dfrac{2-x}{x-1}=\dfrac{m-x}{\left(x-1\right)^2}+1\)
\(\Leftrightarrow-x^2+3x-2=m+x^2-3x+1\)
\(\Leftrightarrow-2x^2+6x-3=m\) (1)
Để từ A kẻ được đúng 1 tiếp tuyến \(\Rightarrow\) (1) có đúng 1 nghiệm thỏa mãn \(x\ne1\)
TH1: (1) có 1 nghiệm bằng 1 và 1 nghiệm khác 1 \(\Rightarrow m=1\)
TH2: đường thẳng \(y=m\) cắt \(y=-2x^2+6x-3\) tại đúng 1 điểm
\(\Rightarrow m=\dfrac{3}{2}\)
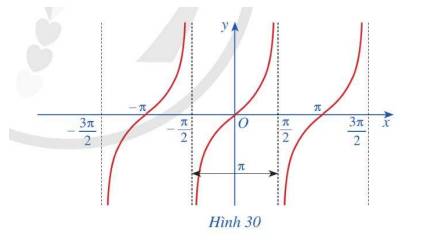
Từ đồ thị hàm số \(y = \tan x\), ta có:
\(\tan x= 0\Leftrightarrow x = k\pi ,\;k \in \mathbb{Z}\)