Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOMN cân tại O có OL là đường cao
nên L là trung điểm của MN
góc ABO=góc OLA=90 độ
=>ABLO nội tiếp
b: Xét ΔABM và ΔANB có
góc ABM=góc ANB
góc BAM chung
=>ΔABM đồng dạng với ΔANB
=>AB/AN=AM/AB
=>AB^2=AN*AM

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
hay A,B,O,C cùng thuộc một đường tròn(1)
Xét tứ giác OIAC có
\(\widehat{OIA}+\widehat{OCA}=180^0\)
Do đó: OIAC là tứ giác nội tiếp
hay O,I,A,C cùng thuộc một đường tròn(2)
Từ (1) và (2) suy ra A,B,O,I,C cùng thuộc một đường tròn
b: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(3)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(4)
Từ (3) và (4) suy ra OA⊥BC(5)
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
hay BC⊥CD(6)
Từ (5) và (6) suy ra CD//OA

do I là trung điểm của MN
⇒I là trung trực của MN
⇒I⊥MN
⇒∠OIM=90⇔∠OIA=90
xét tứ giác ABIO có ∠OBA=∠OIA=90
⇒ABIO nội tiếp
⇒∠BIA=∠AOB (cùng chắn \(\stackrel\frown{AB}\)) (1)
xét tứ giác ACOI có ∠OIA=∠OCA=90
⇒ACOI nội tiếp
⇒∠AIC=∠AOC (cùng chắn \(\stackrel\frown{AC}\)) (2)
xét tứ giác ABOC nội tiếp đường tròn ; AB=AC
⇒∠AOB=∠AOC (chắn 2 cung = nhau) (3)
từ (1);(2);(3) ⇒∠BIA=∠AIC
⇒IA là tia phân giác ∠BIC

a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC

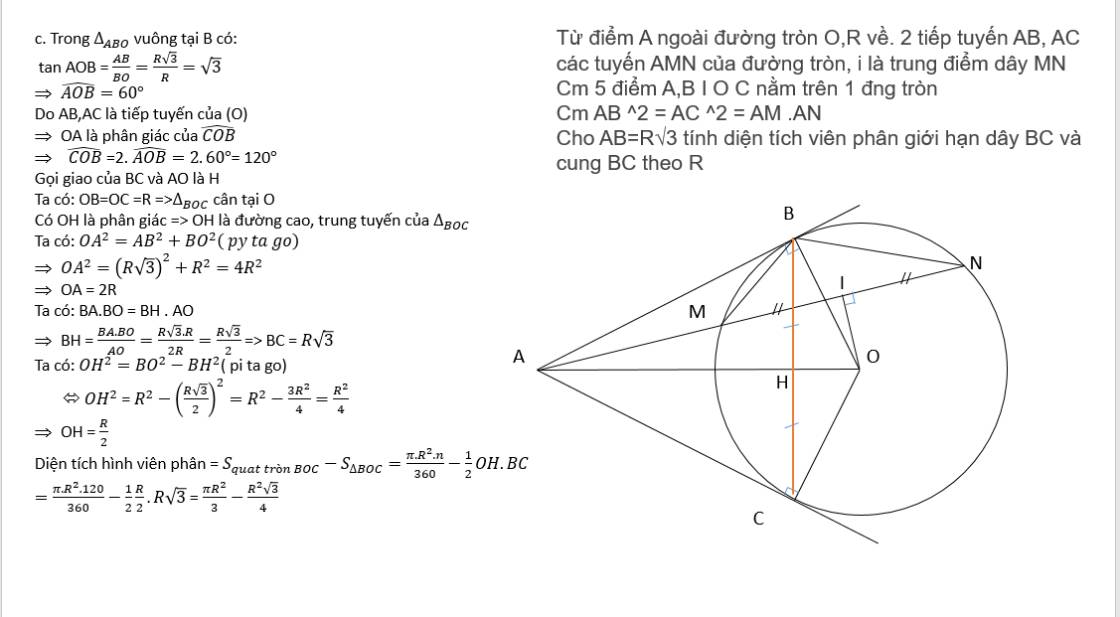
tam giác OAB vuông tại B => 3 điểm O,A,B nằm trên đường tròn đường kính OA (1 )
tam giác OCA vuông tại C => 3 điểm O,A, C nằm trên đường tròn đường kính OA(2)
I là trung điểm NM => OI vuông góc với MN => tam giác OIA vuông tại I => 3 điểm O, I, A nằm trên đường tròn đường kính OA (3 )
từ 1, 2, 3 => 5 điểm A,B,I,O,Ccùng nằm trên 1 đường tròn
b) góc ABM= góc BNM (cùng chắn cung BM); góc BAN chung => tam giác BAN đồng dạng với tam giác MAB
=> AB/AN=AM/AB => AB^2=AM.AN
bạn ơi còn cái ý goc AHM=ANO làm sao vậy