Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi 4 số cần tìm lần lượt là a,b,c,d
theo đề ta có;
\(\frac{\left(a+b+c+d\right)}{4}=45\) (1)
a-2=b:2=c+2=2d
ta đặt: a-2=b:2=c+2=2d=k
suy ra a=k+2;b=2k;c=k-2;d=k:2 (2)
thay (2) vào (1), ta được:
\(\frac{\left(a+b+c+d\right)}{4}=45\)
\(\frac{\left(k+2+2k+k-2+\frac{k}{2}\right)}{4}=45\)
\(\frac{9}{2}k=180\)
\(k=40\)
\(\Rightarrow a=k+2=40+2=42\)
\(\Rightarrow b=2k=2.40=80\)
\(\Rightarrow c=k-2=40-2=38\)
\(\Rightarrow d=\frac{k}{2}=\frac{40}{2}=20\)

Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
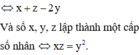
Cách giải:
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
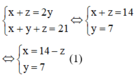
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân nên ta có:
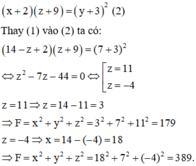



Gọi a, b, c là 3 số. \(\begin{cases}\frac{a+b+c}{3}=20\\\frac{2a+b+c}{3}=24\\\frac{a+3b+c}{3}=32\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}a+b+c=60\\2a+b+c=72\\a+3b+c=96\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}a=12\\b=18\\c=30\end{cases}\)
Vậy, số thứ ba là 30.
Gọi x là số thứ nhất
y là số thứ hai
z là số thứ ba
Theo đề ta có hệ phương trình: \(\begin{cases}x+y+z=60\\2x+y+z=72\\x+3y+z=96\end{cases}\)
Giải hệ phương trình ta được: \(\begin{cases}x=12\\y=18\\z=30\end{cases}\)
Vậy số thứ ba là 30