Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
Sử dụng công thức tính độ dịch chuyển hệ vân:
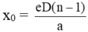
Khoảng vân dịch chuyển 1 đoạn
x = (n - 1).e.D/a = (1,5 - 1).1.3/1,5 = 1 mm

Khi đặt thêm một bản thủy tinh mỏng trước nguồn S1 thì hệ vân sẽ dịch chuyển về phía S1 một đoạn là
\(x = \frac{e(n-1)D}{a}= \frac{12.0,5.1}{1}=6 mm.\)

Khi đặt thêm bản mỏng trước một trong hai khe thì độ dịch của vân trung tâm là
\(x = \frac{e(n-1)D}{a}\)
Vân trung tâm dời tới vị trí của vân sáng bậc 10 tức là
\(x = x_{s10}= 10.i\)
=> \( \frac{e(n-1)D}{a} = 10.\frac{\lambda D}{a}\)
=> \(e(n-1)=10\lambda\)
=> \(n = \frac{10\lambda }{e}+1=\frac{10.0,5}{10}+1=1,5 \)
Chú ý là giữ nguyên đơn vị của \(\lambda (\mu m)\) và \(e (\mu m)\).
Trong thí nghiệm Y- âng về giao thoa, người ta dùng ánh sáng có bước sóng 0,5 μmμm . Đặt một bản thủy tinh mỏng có độ dầy 10 μmμm vào trước một trong hai khe thì thấy vân sáng trung tâm dời tới vị trí của vân sáng bậc 10. Chiết suất của bản mỏng là
A.1,75.
B.1,45.
C.1,5.
D.1,35.

Đáp án A.
Ta có:
x 0 = n - 1 e D a → e = a . x 0 n - 1 D = 9 , 6 μ m

Đáp án: C
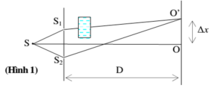
Thời gian truyền qua bản mặt tăng thêm:
![]()
Có thể coi đường truyền qua bản mặt tăng thêm:
![]()
Hiệu đường đi của hai sóng tới điểm có tọa độ x trên màn là:
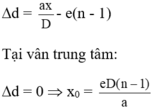

Phương pháp giải : Sử dụng lý thuyết về giao thoa sóng ánh sáng
Cách giải:
Ban đầu tại M có vân sáng bậc 4
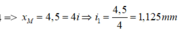
Sau khi dịch mà ra xa => D tăng => i tăng => M chuyển thành vân tối thứ 2 khi đó x M = 2 , 5 i 2 thì khoảng dịch là 0,9m
Ta có:
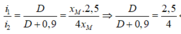
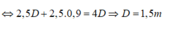
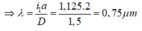
=> Chọn B
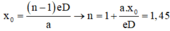
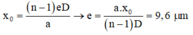
Vân trung tâm sẽ bị dịch chuyển lên phía trên một khoảng là
\(x = \frac{e.(n-1)D}{a}=\frac{10.(1,5-1).2}{0,6}=16,7mm = 1,67cm.\)
Trong thí nghiệm giao thoa ánh sáng khe Y- âng a = 0,6 mm, D = 2 m,λλ = 0,60 μmμm. Đặt ngay sau khe S1 (phía trên) một bản mỏng thủy tinh trong suốt có bề dày 10 μmμm và có chiết suất 1,5. Hỏi vân trung tâm dịch chuyển thế nào?
A.Dịch chuyển lên trên 1,67 mm.
B.Dịch chuyển xuống dưới 1,67 mm.
C Dịch chuyển lên trên 1,67 cm.
D.Dịch chuyển xuống dưới 2,67 mm.