Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Số phẩn tử không gian mẫu là ![]()
Gọi A là biến cố “Hai học sinh A, B ngồi cạnh nhau”.
Chọn 1 bàn để xếp hai học sinh A, B có 15 cách.
Xếp A, B ngổi vào bàn được chọn có 2! cách.
Xếp 28 học sinh còn lại có 28! cách.
Vậy ![]()
Do đó ![]()

Chọn A
Đánh số ba bàn tròn có số chỗ ngồi lần lượt là 6, 7, 8 là bàn 1, bàn 2, bàn 3.
+) Xét phép thử: “Xếp ngẫu nhiên 21 học sinh vào ba bàn tròn 1, 2, 3 nói trên”.
Chọn 6 học sinh trong số 21 học sinh và xếp vào bàn 1 có ![]() cách.
cách.
Chọn 7 học sinh trong số 15 học sinh còn lại và xếp vào bàn 2 có ![]() cách.
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Suy ra số phần tử của không gian mẫu là ![]()
+) Gọi A là biến cố: “ Hai bạn Thêm và Quý luôn ngồi cạnh nhau ”.
Trường hợp 1: Hai bạn Thêm và Quý ngồi bàn 1.
Chọn 4 học sinh từ 19 học sinh còn lại có C 19 4 cách.
Xếp 4 học sinh vừa chọn và hai bạn Thêm, Quý vào bàn 1 có 4!.2! cách.
Chọn 7 học sinh từ 15 học sinh còn lại và xếp vào bàn 2 có ![]() cách.
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Số cách xếp thỏa mãn trường hợp 1 là: ![]()
Trường hợp 2: Hai bạn Thêm và Quý ngồi bàn 2.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 2 là ![]()
Trường hợp 3: Hai bạn Thêm và Quý ngồi bàn 3.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 3 là: ![]()
![]()
![]()
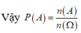
= C 19 4 . 4 ! . 2 ! . C 1 7 . 6 ! . 7 ! + C 19 5 . 5 ! . 2 ! . C 14 6 . 5 ! . 7 ! + C 19 6 . 6 ! . 2 ! . C 13 6 . 5 ! . 6 ! C 21 6 . 5 ! . C 15 7 . 6 ! . 7 ! = 1 10

xếp ngẫu nhiên 8 bạn học sinh vào 4 bàn có 8! cách 40320 cách
=> \(n\left(\Omega\right)=40320\)
Gọi A:" có đúng 2 bàn mà trong đó mỗi bàn gồm 1 nam và 1 nữ "
=> \(n\left(A\right)=C^1_4.C^1_4..4.C^1_3.C^1_3.3.C^2_2.2.C^2_2.1=3456\) cách
=> P(A)= 3456/40320 =3/35

Đáp án A
Xếp 12 học sinh vào 12 ghế có 12! Cách
![]()
Xếp chỗ ngồi cho 2 nhóm học sinh nam – nữ có 2 cách
Trong nhóm có học sinh nam, có 6! Cách sắp xếp 6 học sinh vào 6 chỗ ngồi
Trong nhóm có học sinh nữ, có 6! Cách sắp xếp 6 học sinh vào 6 chỗ ngồi
Suy ra có ![]() cách xếp thỏa mãn bài toán.
cách xếp thỏa mãn bài toán.
Vậy ![]()

Đáp án A
Số cách xếp tuỳ ý là 45!.
Ta tìm số cách xếp thoả mãn; giả sử số ghế của A,B,C lần lượt là a,b,c.
Theo giả thiết có
![]()
Do đó b,c phải cùng chẵn hoặc cùng lẻ.
Nếu b,c chẵn có A 22 2 cách xếp B,C;
1 cách xếp A và 42! cách xếp học sinh khác.
Nếu b,c lẻ có A 23 2 cách xếp B, C;
1 cách xếp A và 42! cách xếp học sinh khác.
Số cách xếp thoả mãn là 42 ! ( A 22 2 + A 23 2 )
Vậy xác suất cần tính
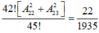

a) Có 2 cách xếp.
Bạn A có 6! cách.
Bạn B có 6! cách.
Đổi vị trí A,B có tất cả 2*(6!)2 cách xếp chỗ.
b) Chọn 1 học sinh A vào vị trí bất kì: 12 cách.
Chọn 1 học sinh B đối diện A có 6 cách.
Cứ chọn liên tục như vậy ta được:
\(\left(12\cdot6\right)\cdot\left(10\cdot5\right)\cdot\left(8\cdot4\right)\cdot\left(6\cdot3\right)\cdot\left(4\cdot2\right)\cdot\left(2\cdot1\right)=2^6\cdot\left(6!\right)^2\)
cách xếp chỗ để hai bạn ngồi đối diện thì kkhasc trường nhau.

+ Số cách xếp 8 học sinh nói trên ngồi xung quanh một bạn tròn là 7 !.
+ Đếm số cách xếp 8 học sinh ngồi xung quanh một bàn tròn mà hai học sinh Hải và Liên ngồi cạnh nhau:
Trước tiên, số cách xếp 7 học sinh (trừ bạn Hải sẽ xếp sau) ngồi xung quanh một bàn tròn là 6 !
Khi đó có 2 cách xếp chỗ ngồi cho bạn Hải (ở bên trái hoặc bên phải bạn Liên).
Theo quy tắc nhân, sẽ có 6!.2 cách xếp 8 bạn ngồi xung quanh một bàn tròn mà hai bạn Hải và Liên ngồi cạnh nhau.
Vậy số cách xếp chỗ ngồi sao cho Hải và Liên không ngồi cạnh nhau là: 7! – 6!.2 =6!.5.
Chọn C.

Chọn C
![]()
Ta có số phần tử không gian mẫu: Ω = 10!.
+) Có 10 cách chọn học sinh cho vị trí số 1. Với mỗi cách chọn vị trí số 1 có 5 cách chọn học sinh cho vị trí số 10 ( Nếu vị trí số 1 là học sinh X thì có 5 cách chọn học sinh ở vị trí 10 là học sinh Y và ngược lại).
+) Có 8 cách chọn học sinh cho vị trí số 2 ( Loại 2 học sinh ở vị trí 10) . Với mỗi cách chọn vị trí số 2 có 4 cách chọn học sinh cho vị trí số 9( Nếu vị trí số 2 là X thì có 4 cách chọn vị trí số 9 là Y, chỉ còn 4 do đã loại 1 em ở lần chọn trước).
+) Hoàn toàn tương tự cho đến hết ta được số phần tử của biến cố cần tính xác suất là: ![]()
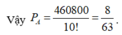

Chọn A
Gọi A là biến cố: Xếp hai học sinh A, B ngồi ở hai bàn xếp cạnh nhau.
Số cách xếp ngẫu nhiên học sinh vào 36 cái bàn là 36!,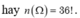
Ta tìm số cách xếp thuận lợi cho biến cố :
- Chọn 1 hàng hoặc 1 cột có C 12 1 cách;
- Mỗi hàng hoặc cột đều có 6 bàn nên có 5 cặp bàn xếp kề nhau, chọn lấy 1 trong 5 cặp bàn cạnh nhau trong hàng hoặc cột vừa chọn ra có C 5 1 cách;
- Xếp A và B vào cặp bàn vừa chọn có 2! cách;
- Xếp 34 học sinh còn lại có 34! cách.
Vậy tổng số cách xếp thoả mãn là: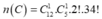
Vậy xác suất cần tính: