Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Điểm M(1;0;0) là 1 điểm thuộc (P)
Vì (P) // (Q) nên
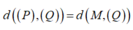
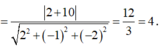
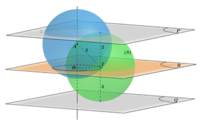
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là:
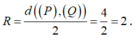
Do đó IA = 2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2.
Ngoài ra
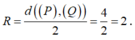
![]()
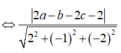
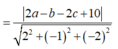
![]()
![]()
![]()
Do đó I luôn thuộc mặt phẳng (R): 2x-y-2z+4=0.
Gọi H là hình chiếu vuông góc của A lên (R). Vì A, (R) cố định nên H cố định.
Ta có
![]()
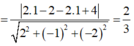
![]()
do đó tam giác AHI vuông tại H nên
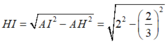
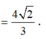
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính
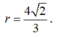

Chọn C
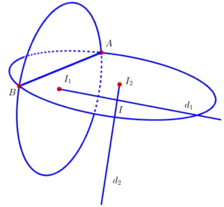
Gọi d1 là đường thẳng đi qua I1 và vuông góc với mặt phẳng (ABI1), khi đó d1 chứa tâm các mặt cầu đi qua đường tròn tâm I1; d2 là đường thẳng đi qua I2 và vuông góc với mặt phẳng (ABI2), khi đó d2 chứa tâm các mặt cầu đi qua đường tròn tâm I2.
Do đó, mặt cầu (S) đi qua cả hai đường tròn tâm (I1) và (I2) có tâm I là giao điểm của d1 và d2 và bán kính R = IA



Đáp Án A
Gọi O là hình chiếu của A lên mp (P)
Ta có ptAO: x = 4 + t y = 6 + t z = 2 + t
⇒ t=-4 ⇒ O(0,2;-2)
Có HB ⊥ AO; HB ⊥ HA ⇒ HB ⊥ (AHO)
⇒ HB ⊥ HO
Ta có B;O cố định
Suy ra H nằm trên đường tròng đường kính OB cố định
⇒ r= 1 2 OB= 6

Đáp án C
Ta có
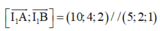
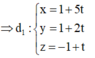
là trục đường tròn tâm I 1 ( 1 ; 1 ; - 1 ) đi qua A, B
Lại có
![]()
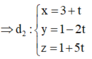
là trục đường tròn tâm I 2 ( 3 ; 1 ; 1 ) đi qua A, B
Tâm mặt cầu (S) chứa cả 2 đường tròn có tâm I ( 8 3 ; 5 3 ; - 2 3 ) là giao điểm của d 1 , d 2
Bán kính mặt cầu cần tìm là R = IA
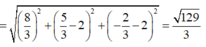

Chọn A
Mặt phẳng (P) chứa đường tròn (C) (giao của 2 mặt cầu đã cho) có phương trình là: 6x + 3y + 2z = 0
Mặt phẳng (P) có phương trình là:
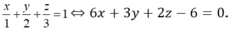
Do đó (P) // (ABC). Mặt cầu (S) tiếp xúc với cả ba đường thẳng AB, BC, CA sẽ giao với mặt phẳng (ABC) theo một đường tròn tiếp xúc với ba đường thẳng AB, BC, CA.
Trên mặt phẳng (ABC) có 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA đó là đường tròn nội tiếp tam giác ABC và ba đường tròn bàng tiếp các góc A, B, C. Do đó có 4 mặt cầu có tâm nằm trên (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA. Tâm của 4 mặt cầu là hình chiếu của tâm 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA lên mặt phẳng (P).

Đáp án B
Phương pháp:
+) Gọi M(x;y;z) tọa độ các véc tơ A M → , B M →
+) Gọi H, K lần lượt là hình chiếu của A,B lên ( α ) , có AMH = BMK
+) Tính sin các góc AMH = BMK và suy ra đẳng thức. Tìm quỹ tích điểm M là một đường tròn.
+) Tính tâm của đường tròn quỹ tích đó.
Cách giải:
Gọi M(x;y;z)
![]()
![]()
Gọi H, K lần lượt là hình chiếu của A, B lên ( α ) có AMH = BMK
![]()
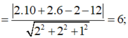
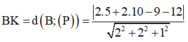
= 3
Khi đó

![]()
Suy ra
![]()
![]()
![]()

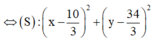
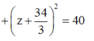

Vậy M ∈ (C) là giao tuyến của ( α ) và (S). Tâm K của (C) là hình chiếu của
I 10 3 ; 34 3 ; - 34 3 trên mặt phẳng ( α ) .
Phương trình đương thẳng đi qua I và vuông góc với ( α ) có dạng
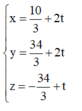
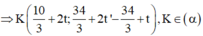
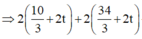
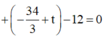
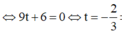
![]()
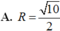
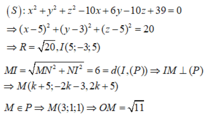


Đáp án đúng : D