Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tâm I ∈ a ⇒ I( 1 + 2t; t; -2t )
I A 2 = I B 2 ⇔ t = - 1 ⇒ I - 1 ; - 1 ; 2 R = I A = 17
Vậy phương trình mặt cầu (S) là x + 1 2 + y + 1 2 + z - 2 2 = 17
x + 1 2 + y + 1 2 + z - 2 2 = 17
Đáp án A

Chọn B.
Phương pháp: Gọi I là tâm mặt cầu thì IM=IN nên I nằm trên mặt phẳng trung trực của MN.
Cách giải: Phương trình mặt phẳng trung trực của MN là


Đáp án C
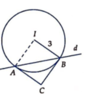
Cắt mặt cầu và 2 tiếp diện bằng một mặt phẳng qua tâm và đường thẳng d. Thiết diện như hình vẽ bên.
ACIB là hình vuông (do I A C ^ = I B C ^ = A C B ^ = 90 ° và I A = I B = I C = R = 3 )
⇒ A B = 3 2

Đáp án B

Mặt cầu (S): x - 1 2 + y - 2 2 + z - 1 2 = 2 có tâm I(1;2;1), R = 2
Xét mặt phẳng thiết diện đi qua tâm I, hai tiếp điểm M, N và cắt d tại H.
Khi đó IH chính là khoảng cách từ điểm I(1;2;1) đến d
Điểm K(2;0;0) ∈ d => I K → = (1;2;1) => f(I;(d)) = I K → ; u d → u d → = 6
Suy ra ![]()
Gọi O là trung điểm của MN
Ta có 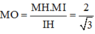
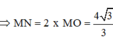

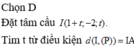


Chọn A.