Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=1+2t\\z=-1+t\end{matrix}\right.\)
Gọi \(M\left(1+2t;1+2t;-1+t\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2t-5;2t+1;t-1\right)\\\overrightarrow{BM}=\left(2t+1;2t+1;t+5\right)\end{matrix}\right.\)
\(\Rightarrow P=\sqrt{\left(2t-5\right)^2+\left(2t+1\right)^2+\left(t-1\right)^2}+\sqrt{\left(2t+1\right)^2+\left(2t+1\right)^2+\left(t+5\right)^2}\)
\(=\sqrt{9t^2-18t+27}+\sqrt{9t^2+18t+27}\)
\(=\sqrt{\left(3-3t\right)^2+18}+\sqrt{\left(3+3t\right)^2+18}\)
\(\ge\sqrt{\left(3-3t+3+3t\right)^2+4.18}=6\sqrt{3}\)

Chọn D
Cách giải:
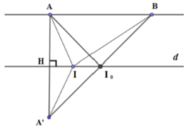
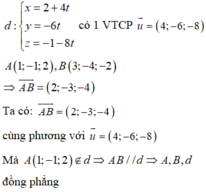
* Xét mặt phẳng chứa AB và d : Gọi A’ là điểm đối xứng của A qua ∆ ; α là mặt phẳng qua A, vuông góc với d
Khi đó, giao điểm H của ∆ với α là trung điểm của AA’

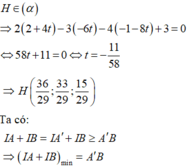
khi và chỉ khi I trùng với I0 là giao điểm của A’B và ∆
HI0 là đường trung bình của tam giác


Đáp án B.
Ta có:
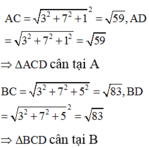
Từ đó gọi M là trung điểm của CD ta có ![]()
Do đó chu vi ∆ A B M là
![]()
(vì AB không thay đổi), tức là khi M là trung điểm cuả CD hay M(0;1;-1)

Đáp án B
Cách giải:
![]()
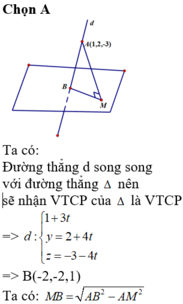
d : x - 2 1 = y - 1 - 2 = z - 1 2 có 1 VTCP v → =(1;-2;2) là một VTCP của ∆
∆ là đường thẳng qua A, vuông góc với d ⇒ ∆ ⊂ ( α ) mặt phẳng qua A và vuông góc d mặt phẳng qua A và vuông góc d
Phương trình mặt phẳng α
![]()
![]()
![]()
khi và chỉ khi đi qua hình chiếu H của B lên α
*) Tìm tọa độ điểm H:
Đường thẳng BH đi qua B(2;0;4) và có VTCP là VTPT của α có phương trình:
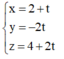
![]()
![]()
![]()
![]()
![]()
![]()

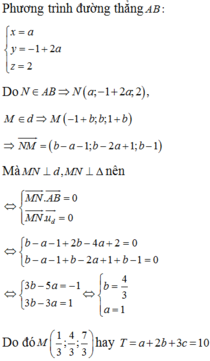

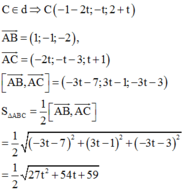
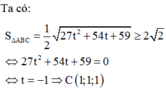
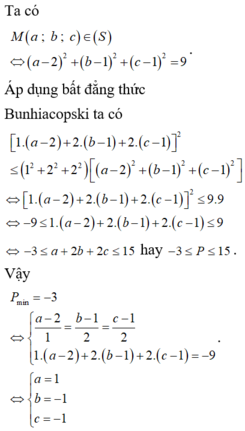




Chọn B