Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

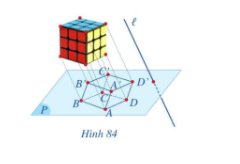
Trường hợp 1: Đặt rubik sao cho các cạnh bên của rubik song song hoặc trùng với đường thẳng ℓ.
Khi đó hình chiếu của rubik trên mp(P) là hình thoi.
Trường hợp 2: Đặt rubik sao cho các cạnh bên của rubik không song song hoặc trùng với đường thẳng ℓ.
Khi đó hình chiếu của rubik trên mp(P) là hình lục giác.
Hình ảnh của khối rubik qua phép chiếu song song lên mặt phẳng (P) theo phương l là hình hộp ABCD.A’B’C’D’

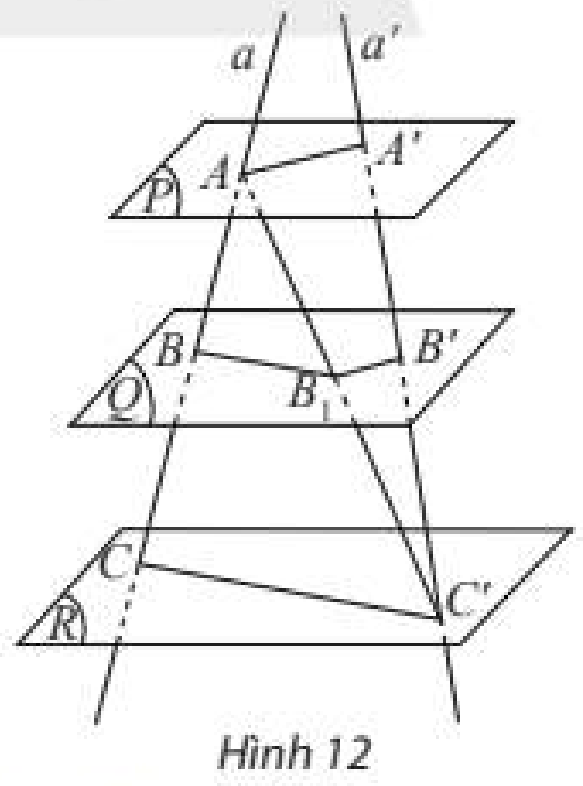
a) Ta có:
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( {ACC'} \right) \cap \left( Q \right) = B{B_1}\\\left( {ACC'} \right) \cap \left( R \right) = CC'\end{array} \right\} \Rightarrow B{B_1}\parallel CC' \Rightarrow \frac{{AB}}{{BC}} = \frac{{A{B_1}}}{{{B_1}C'}}\left( 1 \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( P \right)\parallel \left( Q \right)\\\left( {AA'C'} \right) \cap \left( Q \right) = B{B_1}\\\left( {AA'C'} \right) \cap \left( P \right) = AA'\end{array} \right\} \Rightarrow B{B_1}\parallel AA' \Rightarrow \frac{{A{B_1}}}{{{B_1}C'}} = \frac{{A'B'}}{{B'C'}}\left( 2 \right)\)
c) Từ (1) và (2) suy ra \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AB + BC}}{{A'B' + B'C'}} = \frac{{AC}}{{A'C'}}\)
Vậy \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\).

Ta có:
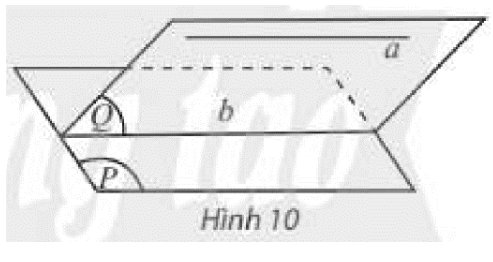
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a'\\\left( P \right) \cap \left( R \right) = b'\end{array} \right\} \Rightarrow a'\parallel b'\)
Vậy nếu \(\left( Q \right)\parallel \left( R \right)\) thì \(a'\parallel b'\); nếu \(\left( Q \right) \equiv \left( R \right)\) thì \(a' \equiv b'\).

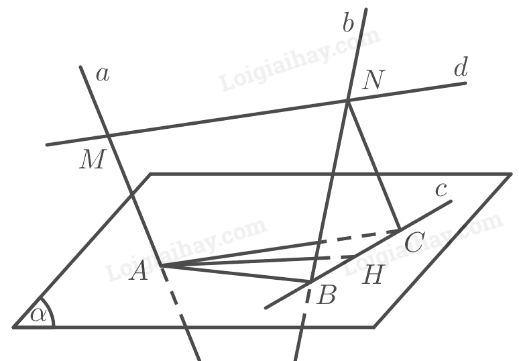
a) Ta có:
\(\left. \begin{array}{l}d \subset \left( {AMNC} \right)\\d\parallel \left( \alpha \right)\\\left( \alpha \right) \cap \left( {AMNC} \right) = AC\end{array} \right\} \Rightarrow d\parallel AC \Rightarrow MN\parallel AC\)
Mà \(a\parallel NC \Rightarrow MA\parallel NC\)
\( \Rightarrow AMNC\) là hình bình hành.
b) Gọi \(\left( \beta \right)\) là mặt phẳng chứa \(b\) và song song với \(a\), \(c = \left( \alpha \right) \cap \left( \beta \right)\)
Ta có:
\(\left. \begin{array}{l}NC\parallel a\\N \in b\end{array} \right\} \Rightarrow NC \subset \left( \beta \right)\)
\( \Rightarrow C \in \left( \alpha \right) \cap \left( \beta \right) \Rightarrow C \in c\)
Vậy điểm \(C\) luôn luôn chạy trên đường thẳng \(c\) là giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) cố định.
c) Trong mặt phẳng \(\left( \alpha \right)\), kẻ \(AH \bot c\)
Vì \(c\) cố định nên \(AC \ge AH\)
\(AMNC\) là hình bình hành \( \Rightarrow MN = AC\)
Vậy \(MN \ge AH\)
Vậy \(MN\) nhỏ nhất khi \(C \equiv H\). Khi đó \(d\parallel AH\).

Gọi (R) là mặt phẳng chứa a và (R)//(Q)
(Q)//(R)
\(\left(P\right)\cap\left(Q\right)=a'\)
\(\left(P\right)\cap\left(R\right)=a\)
Do đó: a//a'
mà IJ vuông góc a
nên JI vuông góc a'
\(\left(P\right)\perp\left(Q\right)\)
\(\left(P\right)\cap\left(Q\right)=a'\)
\(JI\perp a\)
Do đó: JI vuông góc (Q)
=>IJ vuông góc b
tham khảo:
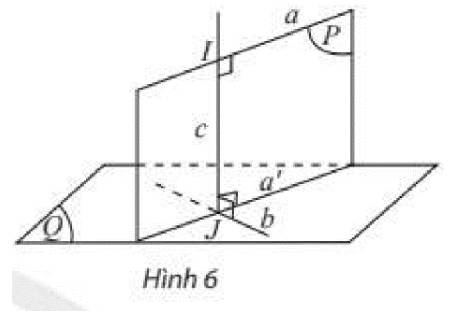
Gọi (R) là mặt phẳng chứa a song song với (Q).
(P) cắt hai mặt phẳng song song tại a và a' nên a//a'
Trong mặt phẳng (P), IJ⊥a,a//a′ nên IJ⊥a′
Ta có: (P)⊥(Q), (P) cắt (Q) tại a', IJ⊥a′ nên IJ⊥(P)
Suy ra IJ⊥b

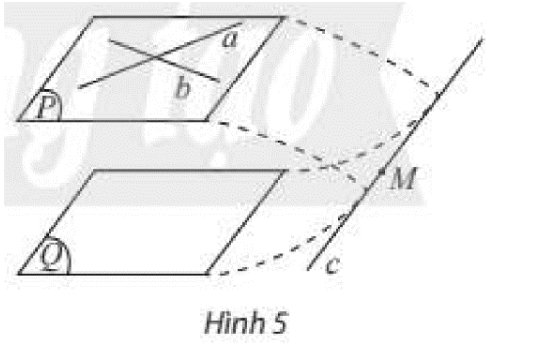
a) Gọi \(I\) là giao điểm của \(a\) và \(b\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}a\parallel \left( Q \right)\\\left( P \right) \supset a\\\left( P \right) \cap \left( Q \right) = c\end{array} \right\} \Rightarrow c\parallel a\\\left. \begin{array}{l}b\parallel \left( Q \right)\\\left( P \right) \supset b\\\left( P \right) \cap \left( Q \right) = c\end{array} \right\} \Rightarrow c\parallel b\end{array}\)
Do đó qua \(I\) ta kẻ được hai đường thẳng \(a\) và \(b\) cùng song song với \(c\), mâu thuẫn với định lí qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.
Vậy \(c\) phải cắt ít nhất một trong hai đường thẳng \(a,b\).
Nếu đường thẳng \(c\) cắt đường thẳng \(a\) hoặc đường thẳng \(b\), mà đường thẳng \(c\) nằm trong mặt phẳng \(\left( Q \right)\), khi đó đường thẳng \(a\) hoặc đường thẳng \(b\) có 1 điểm chung với mặt phẳng \(\left( Q \right)\). Điều này trái với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\).
b) Vì \(\left( P \right)\) chứa đường thẳng \(a\) mà \(a\) song song với mặt phẳng \(\left( Q \right)\) nên \(\left( P \right)\) và \(\left( Q \right)\) là hai mặt phẳng phân biệt.
Theo chứng minh ở trên, nếu \(\left( P \right)\) và \(\left( Q \right)\) có điểm chung \(M\) thì mâu thuẫn với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\).
Vậy hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) không có điểm chung.

a) Giả sử A'=(x'; y'). Khi đó \(T_{\overrightarrow{v}}\left(A\right)=A'\Leftrightarrow\left\{{}\begin{matrix}x'=3-1=2\\y'=5+2=7\end{matrix}\right.\)
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có: \(A=T_{\overrightarrow{v}}\left(C\right)\Leftrightarrow C=^T\overrightarrow{-v}\left(A\right)=\left(4;3\right)\)
c) Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = \(^T\overrightarrow{v}\) =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy \(^T\overrightarrow{v}\) (d) = d'.
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi \(^T\overrightarrow{v}\)(d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó \(^T\overrightarrow{v}\) (B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8.
a) Giả sử A'=(x'; y'). Khi đó
(A) = A' ⇔
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có A = (C) ⇔ C=
(A) = (4;3)
c)Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy
(d) = d'
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi (d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó
(B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8
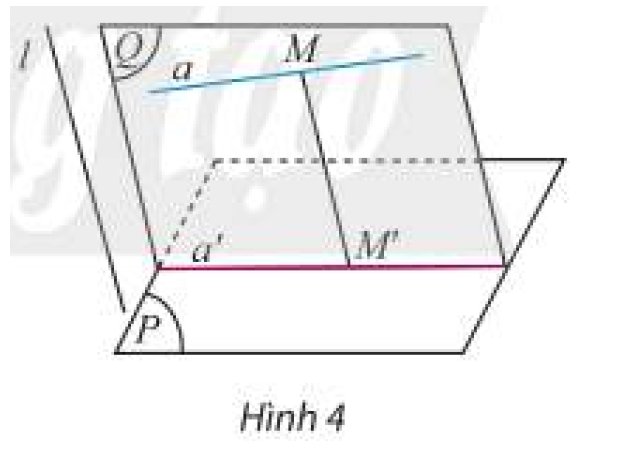


a: M' thay đổi trên a'
b: Ảnh của a qua phép chiếu theo phương l trên mp(P) là đường thẳng a'