Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(u=Acos\left(\dfrac{2\pi}{T}t-\dfrac{2\pi x}{\lambda}\right)\)
Khoảng cách giữa hai điểm gần nhau nhất dao động cùng pha là λ và khoảng cách giữa hai điểm gần nhau nhất dao động ngược pha là \(\dfrac{\lambda}{2}\)

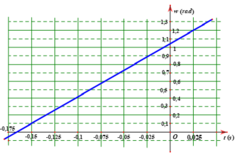
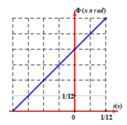
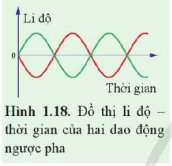
Hai dao động đều có chu kì `T` và thời điểm `t=0` tại vị trí cân bằng, nhưng tại cùng thời điểm tiếp theo thì:
- Dao động màu xanh đến biên dương.
- Dao động màu hồng đến biên âm.
Mà từ biên dương đến biên âm chênh lệch 1 góc `\pi`.
`=>` Độ lệch pha của hai dao động là: `\pi (rad)`

a) Vì hai điểm gần nhất trên cùng phương truyền sóng dao động lệch pha nhau một góc \(\dfrac{\pi}{2}\)
Khoảng cách giữa hai điểm là 360cm= \(\dfrac{3\lambda}{2}\) nên hai điểm này dao động ngược pha nhau độ lệch pha của chúng là π
b) Sau 0,1s sóng truyền được khoảng cách là 0,1.330 = 33m = \(\dfrac{55\lambda}{4}\)
Độ lệch pha là \(\dfrac{3\pi}{4}\)

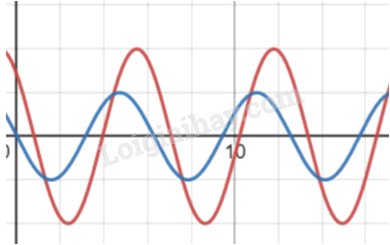
Dao động 1 vẽ với biên độ A và chu kì T
Dao động 2 có cùng chu kì với dao động 1 và biên độ \(A_2=2A\) vị trí đầu tiên của dao động thứ hai bằng \(\dfrac{\sqrt{2}}{2}A_2\) và ở thời điểm \(\dfrac{T}{8}\) thì dao động 2 sẽ đi qua vị trí cân bằng.
Cứ thế tiếp tục vẽ 2 chu kì dao động của hai dao động
Đường màu xanh là dao động thứ nhất, đường màu đỏ là dao động thứ 2
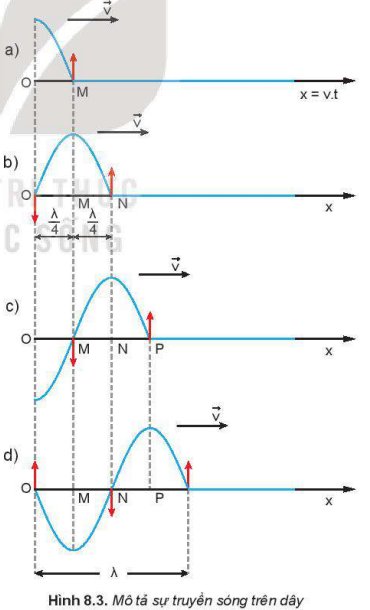

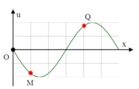
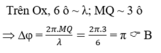
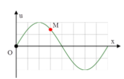

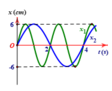

Từ đồ thị ta có thể thấy điểm M đang ở lõm sóng (tạm gọi là biên âm), điểm N đang ở VTCB, điểm P đang ở ngọn sóng (tạm gọi là biên dương).
Nên 2 cặp điểm M và N, N và P dao động lệch phaformat('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%222.5%22%20x2%3D%2218.5%22%20y1%3D%2220.5%22%20y2%3D%2220.5%22%2F%3E%3Ctext%20font-family%3D%22math1437d7d1d97917cd627a34a6a0f%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2210.5%22%20y%3D%2216%22%3E%26%23x3C0%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2210.5%22%20y%3D%2237%22%3E2%3C%2Ftext%3E%3C%2Fsvg%3E)
Còn điểm M và điểm P dao động ngược pha nhau.