Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì: \(AB=\dfrac{\lambda}{4}\)
Độ lệch pha của hai điểm là:
\(\Delta\varphi=\dfrac{2\pi}{\lambda}AB=\dfrac{2\pi}{\lambda}\cdot\dfrac{\lambda}{4}=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\) rad

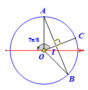
\(MA=6cm;MB=AB-MA=20-6=14cm\)
\(AM\perp MC\Rightarrow AC=\sqrt{AM^2+MC^2}=\sqrt{6^2+8^2}=10cm\)
\(BM\perp MC\Rightarrow BC=\sqrt{BM^2+MC^2}=\sqrt{14^2+8^2}=2\sqrt{65}cm\)
Xét một điểm N bất kì trên CM ta có: \(d_2-d_1=k\lambda\)
Hai nguồn dao động cùng pha:
\(\Rightarrow\left\{{}\begin{matrix}d_2-d_1=\left(k+0,5\right)\lambda\\BC-AC\le k\lambda\le BM-AM\end{matrix}\right.\)
\(\Rightarrow2\sqrt{65}-10\le k+0,5\le14-6\Rightarrow5,62\le k\le7,5\)
\(\Rightarrow k=\left\{6,5;7,5\right\}\)
Vậy có hai điểm cực tiểu trên CD.

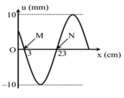


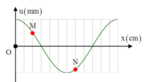

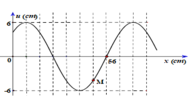
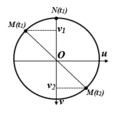

a) Vì hai điểm gần nhất trên cùng phương truyền sóng dao động lệch pha nhau một góc \(\dfrac{\pi}{2}\)
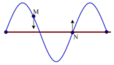
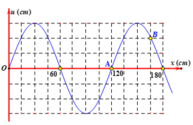
Khoảng cách giữa hai điểm là 360cm= \(\dfrac{3\lambda}{2}\) nên hai điểm này dao động ngược pha nhau độ lệch pha của chúng là π
b) Sau 0,1s sóng truyền được khoảng cách là 0,1.330 = 33m = \(\dfrac{55\lambda}{4}\)
Độ lệch pha là \(\dfrac{3\pi}{4}\)