K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KN
6
PT
1
LN
10
DT
Dang Tung
CTVHS
12 tháng 6 2023
a) \(1\dfrac{5}{7}=\dfrac{12}{7}=\dfrac{24}{14},1\dfrac{6}{7}=\dfrac{13}{7}=\dfrac{26}{14}\)
Gọi SPT là : x
Ta có : \(\dfrac{24}{14}< x< \dfrac{26}{14}\\ x=\dfrac{25}{14}\)
b) Gọi SPT là : x
\(\dfrac{1}{3}< x< \dfrac{2}{3}\\=> \dfrac{5}{15}< x< \dfrac{10}{15}\\ =>x\in\left\{\dfrac{6}{15};\dfrac{7}{15};\dfrac{8}{15};\dfrac{9}{15}\right\}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 6 2023
a,\(\dfrac{5}{7}\) = \(\dfrac{1\times7+5}{7}=\dfrac{12}{7}\) = \(\dfrac{12\times2}{7\times2}\)=\(\dfrac{24}{14}\)
1\(\dfrac{6}{7}\)=\(\dfrac{1\times7+6}{7}=\dfrac{13}{7}\)= \(\dfrac{13\times2}{7\times2}\) = \(\dfrac{26}{14}\)
Phân số lớn hơn 1\(\dfrac{5}{4}\) và bé hơn 1\(\dfrac{6}{7}\) là phân số nằm giữa hai phân số
\(\dfrac{24}{14}\) và \(\dfrac{26}{14}\) đó là phân số \(\dfrac{25}{14}\)
b, \(\dfrac{1}{3}=\dfrac{1\times3}{3\times3}\) = \(\dfrac{3}{9}\); \(\dfrac{2}{3}\) = \(\dfrac{2\times3}{3\times3}\) = \(\dfrac{6}{9}\)
Hai phân số lớn hơn \(\dfrac{1}{3}\) và bé hơn \(\dfrac{2}{3}\) là hai phân số nằm giữa hai phân số \(\dfrac{3}{9}\) và \(\dfrac{6}{9}\) lần lượt là: \(\dfrac{4}{9}\) và \(\dfrac{5}{9}\)
ta có bốn phân số trên sắp xếp theo thứ tự tăng dần là:
\(\dfrac{3}{9};\) \(\dfrac{4}{9}\); \(\dfrac{5}{9}\); \(\dfrac{6}{9}\) và 4 phân số đều có tử số là các số tự nhiên liến tiếp.
Vậy hai phân số thỏa mãn đề bài là: \(\dfrac{4}{9}\); \(\dfrac{5}{9}\)
Đáp số: a, \(\dfrac{25}{14}\); b, \(\dfrac{4}{9}\); \(\dfrac{5}{9}\)
1 tháng 4 2021
a) Gọi phân số cần tìm có dạng là \(\dfrac{a}{12}\)
Theo đề, ta có: \(\dfrac{-2}{3}< \dfrac{a}{12}< \dfrac{-1}{4}\)
\(\Leftrightarrow\dfrac{-8}{12}< \dfrac{a}{12}< \dfrac{-3}{12}\)
\(\Leftrightarrow-8< a< -3\)
\(\Leftrightarrow a\in\left\{-7;-6;-5;-4\right\}\)
Vậy: Các phân số cần tìm là \(\dfrac{-7}{12};\dfrac{-6}{12};\dfrac{-5}{12};\dfrac{-4}{12}\)
1 tháng 4 2021
b) Gọi phân số cần tìm có dạng là \(\dfrac{15}{a}\left(a\ne0\right)\)
Theo đề, ta có: \(\dfrac{3}{7}< \dfrac{15}{a}< \dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{15}{35}< \dfrac{15}{a}< \dfrac{15}{24}\)
Vậy: Các phân số cần tìm là \(\dfrac{15}{34};\dfrac{15}{33};...;\dfrac{15}{25}\)
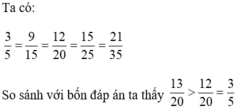
Chọn đáp án C