Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Xét tứ diện ABCD suy ra “ Số các đỉnh hoặc các mặt của bất kì hình đa diện nào cũng lớn hơn hoặc bằng 4

a,5 đường thẳng cắt nhau tại 1 điểm tạo thành 10 tia chung gốc
Mỗi tia tạo với 9 tia còn lại thành 9 góc mà có 10 tia như vậy tì số góc được tạo thành là :
9 . 10 = 90 ( góc )
Vì mỗi góc được lặp lại 2 lần nên có tất cả :
90 : 2 = 45 ( góc )
b, 5 đường thẳng cắt nhau tạo thành 5 góc bẹt . Vậy có tất cả :
45 - 5 = 40 góc khác góc bẹt
Có 40 góc khác góc bẹt mà mỗi góc có 1 góc đối đỉnh với nó nên có tất cả :
40 : 2 = 20 ( cặp góc đối đỉnh )
c, 5 đường thẳng cắt nhau tạo thành 10 góc không có điểm chung
\(\Rightarrow\) Tổng 10 góc này là 360 độ
- Giả sử 10 góc này đều nhỏ hơn 36 độ
\(\Rightarrow\) Tổng của 10 góc này nhỏ hơn 360 độ ( vô lý )
\(\Rightarrow\) Trong 10 góc này tồn tại ít nhất 1 góc lớn hơn 36 độ
- Giả sử 10 góc này đều lơn hơn 36 độ
\(\Rightarrow\) Tổng của 10 góc này lớn hơn 360 độ ( vô lý )
\(\Rightarrow\) Trong 10 góc này tồn tại ít nhất 1 góc nhỏ hơn hoặc = 36 độ
a) Năm đường thẳng cắt nhau tại 1 điểm tạo thành 10 tia chung gốc.
Mỗi tia tạo với 9 tia còn lại 9 góc mà có 10 tia như vậy nên có tất cả số góc là:
9 x 10 = 90 ( góc )
Vì mỗi góc được tính lặp lại 2 lần nên:
90 : 2 = 45 ( góc )
b) 5 đường thẳng cắt nhau tạo thành 5 góc bẹt. Vậy có tất cả số góc khác góc bẹt là:
45 - 5 = 40 ( góc khác góc bẹt )
Có tất cả 40 góc khác góc bẹt mà mỗi góc có 1 góc đối đỉnh với nó. Nên có tất cả :
40 : 2 = 20 ( cặp góc đối đỉnh )
c) Năm đường thẳng cắt nhau tạo thành 10 góc không có điểm trong chung.
=> Tổng của 10 góc này bằng 360o
Giả sử cả 10 góc đều bé hơn 36o
=> Tổng của 10 góc này < 360o ( điều này là vô lý )
=> Trong 10 góc này tồn tại ít nhất 1 góc nhỏ hơn 36o

Đáp án A
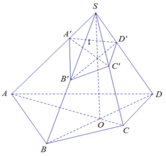
Xác định mặt phẳng (A’B’C’D’)
Lấy A’, B’, C’ lần lượt nằm trên SA, SB, SC
⇒ D’ thuộc mặt phẳng (A’B’C’)
Gọi O = AC ∩ BD
Trong (SAC) có: I = SO ∩ A ' C '
Trong (SBD) có: B ' I ∩ SD = D '
Từ cách dựng mặt phẳng (A’B’C’D’) ta thấy: SO, A’C’, B’D’ đồng quy tại I

A. (SAC) ∩ (SBD) = SO
B. (SAB) ∩ (SCD) = SE
C. (SAD) ∩ (SBC) = xy
D. nếu S, A, C, D cùng nằm trong một mặt phẳng thì S ∈ (ACD) mâu thuẫn với giả thiết S.ABCD là hình chóp
Đáp án D

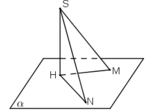
Giả sử ta có hai đường xiên SM, SN và các hình chiếu HM, HN của chúng trên mp (α).
Vì SH ⊥ mp(α)
⇒ SH ⊥ HM và SH ⊥ HN
⇒ ΔSHN và ΔSHM vuông tại H.
Áp dụng định lí Py-ta- go vào hai tam giác vuông này ta có:
⇒ S M 2 = S H 2 + H M 2 ; v à S N 2 = S H 2 + H N 2 . a ) S M = S N ⇔ S M 2 = S N 2 ⇔ H M 2 = H N 2 ⇔ H M = H N . b ) S M > S N ⇔ S M 2 > S N 2 ⇔ H M 2 > H N 2 ⇔ H M > H N .

Đáp án D
Xét tứ diện đều ABCD với đỉnh A là đỉnh chung của đúng 3 cạnh m=4

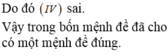
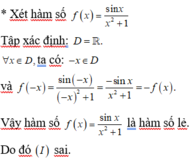
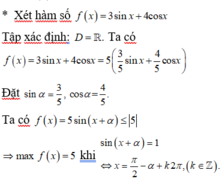

Đáp án A
Số các đỉnh hoặc các mặt của bất kì hình đa diện nào cũng lớn hơn hoặc bằng 4 ( tứ diện có 4 đỉnh và 4 mặt ).