Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

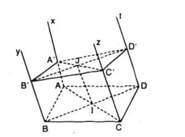
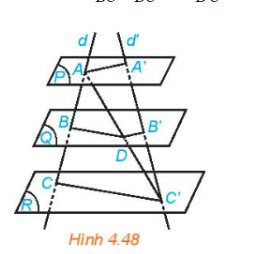
a) Do ABCD là hình bình hành, nên AB // DC
=> AB // (Cz, Dt) (1)
Theo giả thiết Ax // Dt nên Ax // (Cz, Dt) (2)
Từ (1) và (2) suy ra: (Ax, By) // (Cz, Dt)
b) Mặt phẳng β cắt 2 mặt phẳng song song ( Ax, By), (Cz, Dt) theo hai giao tuyến là A’B’và C’D’ nên A’B’// C’D’. (3)
Chứng minh tương tự (Ax, Dt) song song với (By,Cz).Và mặt phẳng β cắt 2 mặt phẳng song song (Ax, Dt), (By, Cz) theo hai giao tuyến là A’D’và B’C’ nên A’D’// B’C’ (4)
Từ (3) và (4) suy ra: tứ giác A’B’C’D’ là hình bình hành.
=> J là trung điểm của A’C’ ( tính chất hình bình hành).
Tứ giác AA’C’C là hình thang vì có: AA’ // CC’ ( giả thiết). Lại có, I và J lần lượt là trung điểm của AC và A’C’ nên IJ là đường trung bình của hình thang
=> IJ// AA’// CC’ ( đpcm).
c) Vì IJ là đường trung bình của hình thang ACC’A’ nên IJ = 1/2(AA’ + CC’)
IJ cũng là đường trung bình của hình thang BDD’B’: IJ = 1/2(BB’ + DD’)
Từ đây suy ra: DD’ + BB’ = AA’ + CC’
=> DD’ = AA’ + CC’ – BB’ = a + c – b

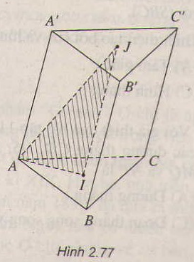
a) Mặt phẳng (Q) và (R) song song với nhau, suy ra giao tuyến của (ACC') với hai mặt phẳng (Q) và (R) song song với nhau. Do đó BD // CC'
Mặt phẳng (Q) và (P) song song với nhau, suy ra giao tuyến của (C'AA') với hai mặt phẳng (Q) và (P) song song với nhau. Do đó B'D // AA'
b) Xét tam giác ACC' ta có BD // CC' suy ra \(\frac{{AD}}{{BC}} = \frac{{AD}}{{DC'}}\)
Xét tam giác C'AA' ta có B'D // AA' suy ra \(ADDC' = A'B'B'C'\)
Do đó, \(\frac{{AB}}{{BC'}} = \frac{{AD}}{{DC'}} = \frac{{A'B'}}{{B'C'}}\)

a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.

Đáp án C
Mặt phẳng (P) đi qua A’ và song song AC
Trong mặt phẳng (SAC), ta có A’C’//AC (A’C’ là đường trung bình tam giác SAC)
⇒ (P) đi qua A’C’ cố định

Câu 1:
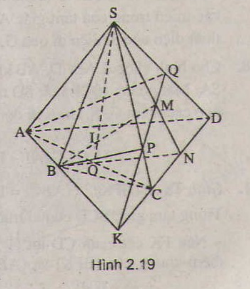
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ
Câu 2:
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE)
b) Chứng minh M ∈ (SDC), trong (SDC) : MC' ∩ SD = F. Chứng minh thiết diện là AEC'F
Câu 3:
a) Chứng minh E, N là hai điểm chung của mặt phẳng (PMN) và (BCD)
b) EN ∩ BC = Q. Chứng minh Q là điểm cần tìm
Câu 4:
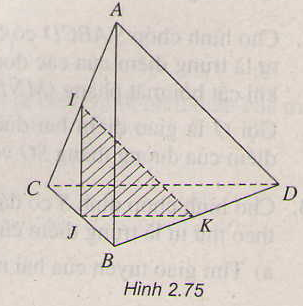
a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm
Câu 5:
a) Trong mặt phẳng (α) vì AB và CD không song song nên AB ∩ DC = E
=> E ∈ DC, mà DC ⊂ (SDC)
=> E ∈ ( SDC). Trong (SDC) đường thẳng ME cắt SD tại N
=> N ∈ ME mà ME ⊂ (MAB)
=> N ∈ ( MAB). Lại có N ∈ SD => N = SD ∩ (MAB)
b) O là giao điểm của AC và BD => O thộc AC và BD, mà AC ⊂ ( SAC)
=> O ∈( SAC), BD ⊂ (SBD) , O ∈ (SBD)
=> O là một điểm chung của (SAC) và (SBD), mặt khác S cũng là điểm chung của (SAC) và (SBD) => (SAC) ∩ (SBD) = SO
Trong mặt phẳng (AEN) gọi I = AM ∩ BN thì I thuộc AM và I thuộc BN
Mà AM ⊂ (SAC) => I ∈ (SAC), BN ⊂ ( SBD) => I ∈ (SBD). Như vậy I là điểm chung của (SAC) và (SBD) nên I thuộc giao tuyến SO của (SAC) và (SBD) tức là S, I, O thẳng hàng hay SO, AM, BN đồng quy

Gọi O là trung điểm của AC
Hình bình hành ACC'A' có: OO' // AA'
Vì O thuộc (ABCD)
Do đó: O là ảnh của O'.

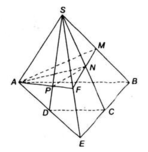
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
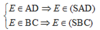
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.

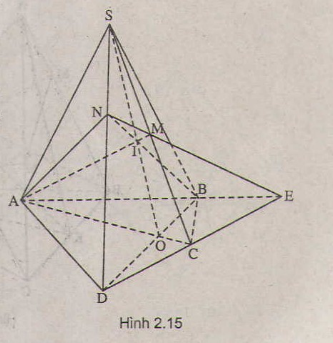
Đáp án A
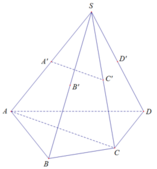
Xác định mặt phẳng (A’B’C’D’)
Lấy A’, B’, C’ lần lượt nằm trên SA, SB, SC
⇒ D’ thuộc mặt phẳng (A’B’C’)
Gọi O = AC ∩ BD
Trong (SAC) có: I = SO ∩ A ' C '
Trong (SBD) có: B ' I ∩ SD = D '
Từ cách dựng mặt phẳng (A’B’C’D’) ta thấy: SO, A’C’, B’D’ đồng quy tại I