Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: B là ảnh của A' lên (ABCD)
Có: D'C // A'B nên C là ảnh của D' lên (ABCD)
Từ C' kẻ C'E // CD' // A'B. Suy ra E là ảnh của C' lên (ABCD).
Vậy tam giác BCE là ảnh của tam giác A'C'D' qua phép chiếu song song lên mặt phẳng (ABCD) theo phương A'B.

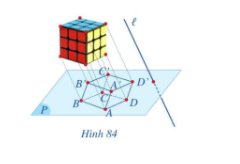
Trường hợp 1: Đặt rubik sao cho các cạnh bên của rubik song song hoặc trùng với đường thẳng ℓ.
Khi đó hình chiếu của rubik trên mp(P) là hình thoi.
Trường hợp 2: Đặt rubik sao cho các cạnh bên của rubik không song song hoặc trùng với đường thẳng ℓ.
Khi đó hình chiếu của rubik trên mp(P) là hình lục giác.
Hình ảnh của khối rubik qua phép chiếu song song lên mặt phẳng (P) theo phương l là hình hộp ABCD.A’B’C’D’


Nhìn hình vẽ ta thấy: A'B'C'D' là hình chiếu song song của hình bình hành ABCD trên mặt phẳng (P) theo phương l.

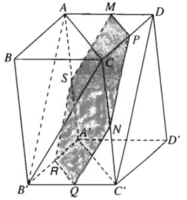
a) Vẽ MP song song với AC và cắt CD tại P
Ta có: 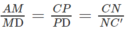
Do đó PN // DC′ // AB′
Đường thẳng MN thuộc mặt phẳng (MNP) và mặt phẳng này có MP // AC và PN // AB′. Vậy mặt phẳng(MNP) song song với mặt phẳng (ACB’) và do đó MN // (ACB′)
b) Vì mặt phẳng (MNP) song song với mặt phẳng (ACB’) nên hai mặt phẳng đó cắt các mặt bên của hình hộp theo các giao tuyến song song.
Ta vẽ NQ // CB′, QR // C′A′ ((// CA), RS //AB′ (//PN) và tất nhiên SM // QN. Thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’) là hình lục giác MPNQRS có các cạnh đối diện song song với nhau từng đôi một: MP // RQ, PN //SR, NQ // MS.

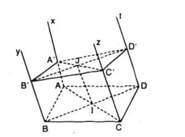
a) Do ABCD là hình bình hành, nên AB // DC
=> AB // (Cz, Dt) (1)
Theo giả thiết Ax // Dt nên Ax // (Cz, Dt) (2)
Từ (1) và (2) suy ra: (Ax, By) // (Cz, Dt)
b) Mặt phẳng β cắt 2 mặt phẳng song song ( Ax, By), (Cz, Dt) theo hai giao tuyến là A’B’và C’D’ nên A’B’// C’D’. (3)
Chứng minh tương tự (Ax, Dt) song song với (By,Cz).Và mặt phẳng β cắt 2 mặt phẳng song song (Ax, Dt), (By, Cz) theo hai giao tuyến là A’D’và B’C’ nên A’D’// B’C’ (4)
Từ (3) và (4) suy ra: tứ giác A’B’C’D’ là hình bình hành.
=> J là trung điểm của A’C’ ( tính chất hình bình hành).
Tứ giác AA’C’C là hình thang vì có: AA’ // CC’ ( giả thiết). Lại có, I và J lần lượt là trung điểm của AC và A’C’ nên IJ là đường trung bình của hình thang
=> IJ// AA’// CC’ ( đpcm).
c) Vì IJ là đường trung bình của hình thang ACC’A’ nên IJ = 1/2(AA’ + CC’)
IJ cũng là đường trung bình của hình thang BDD’B’: IJ = 1/2(BB’ + DD’)
Từ đây suy ra: DD’ + BB’ = AA’ + CC’
=> DD’ = AA’ + CC’ – BB’ = a + c – b

Gọi K=AM∩SOK=AM∩SO. Mặt phẳng (P) đi qua K và song song với BD nên cắt (SBD) theo giao tuyế d' đi qua K và song song với BD. Vậy qua K, ta vẽ d' song song với BD. Đường thẳng d' cắt SB và SD lần lượt tại E và F. Đây là các điểm cần tìm.

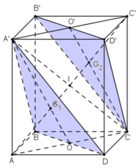
a) + A’D’ // BC và A’D’ = BC
⇒ A’D’CB là hình bình hành
⇒ A’B // D’C, mà D’C ⊂ (B’D’C) ⇒ A’B // (B’D’C) (1)
+ BB’ // DD’ và BB’ = DD’
⇒ BDD’B’ là hình bình hành
⇒ BD // B’D’, mà B’D’ ⊂ (B’D’C) ⇒ BD // (B’D’C) (2)
A’B ⊂ (BDA’) và BD ⊂ (BDA’); A’B ∩ BD = B (3)
Từ (1), (2), (3) suy ra : (BDA’) // (B’D’C).
b) Gọi O = AC ∩ BD
+ Ta có: O ∈ AC ⊂ (AA’C’C)
⇒ A’O ⊂ (AA’C’C).
Trong (AA’C’C), gọi A’O ∩ AC’ = G1.
G1 ∈ A’O ⊂ (A’BD)
⇒ G1 ∈ AC’ ∩ (BDA’).
+ Trong hình bình hành AA’C’C gọi I = A’C ∩ AC’
⇒ A’I = IC.
⇒ AI là trung tuyến của ΔA’AC
⇒ G 1 = A ’ O ∩ A C ’ là giao của hai trung tuyến AI và A’O của ΔA’AC
⇒ G 1 là trọng tâm ΔA’AC
⇒ A ’ G 1 = 2 . A ’ O / 3
⇒ G 1 cũng là trọng tâm ΔA’BD.
Vậy AC' đi qua trọng tâm G 1 của ΔA’BD.
Chứng minh tương tự đối với điểm G 2 .
c) *Vì G 1 là trọng tâm của ΔAA’C nên A G 1 / A I = 2 / 3 .
Vì I là trung điểm của AC’ nên AI = 1/2.AC’
Từ các kết quả này, ta có : A G 1 = 1 / 3 . A C ’
*Chứng minh tương tự ta có : C ’ G 2 = 1 / 3 . A C ’
Suy ra : A G 1 = G 1 G 2 = G 2 C ’ = 1 / 3 . A C ’ .
d) (A’IO) chính là mp (AA’C’C) nên thiết diện cần tìm chính là hình bình hành AA’C’C.


Gọi O là trung điểm của AC
Hình bình hành ACC'A' có: OO' // AA'
Vì O thuộc (ABCD)
Do đó: O là ảnh của O'.