

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

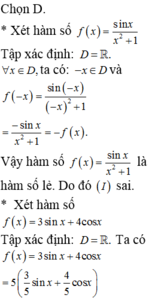

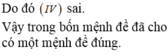

Đáp án B
+ Xét hàm y = f(x) = cos (x + π)
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-x + π) = -cos x = cos (x + π) = f(x)
Do đó y = cos (x + π) là hàm số chẵn .
+ Xét hàm y = g(x) = tan2016x
TXĐ: D = R\{π/2 + kπ, k ∈ Z}
Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = tan2016(-x) = (-tan x)2016 = tan2016x = g(x)
Do đó: y = tan2016x là hàm chẵn trên tập xác định của nó.
+Xét hàm y = cot2x
f(-x) = cot(-2x) = - cot 2x = -f(x) nên đây là hàm số lẻ.
+ Xét hàm số y = 1-sinx
f(-x) = 1- sin(-x) = 1+ sin x
Nên hàm số không chẵn không lẻ

Đáp án B
- Hàm số xác định với mọi x ∈ R.
- Hàm số đã cho liên tục với mọi x ≠ 1.
- Ta có:
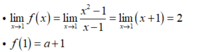
- Để hàm số liên tục tại x= 1 khi và chỉ khi:
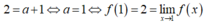
- Vậy với a = 1 thì hàm số đã cho liên tục tại x = 1. Do đó, hàm số liên tục trên R.

Đáp án A
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f (x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
Phản ví dụ
Lấy hàm f ( x ) = x ta có D= R nên hàm số f(x) liên tục trên R.
Nhưng ta có l i m x → 0 + f ( x ) - f ( 0 ) x - 0 = l i m x → 0 + x - 0 x - 0 = l i m x → 0 + x - 0 x - 0 = 1 l i m x → 0 - f ( x ) - f ( 0 ) x - 0 = l i m x → 0 - x - 0 x - 0 = l i m x → 0 - - x - 0 x - 0 = - 1
Nên hàm số không có đạo hàm tại x = 0.
Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.