Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Khoảng cách giữa hai vị trí cân bằng của một bụng sóng với một nút sóng cạnh nhau là 0,25λ = 6 cm → λ = 24 cm.
→ Chu kì của sóng T = λ/v = 0,24/1,2 = 0,2 s.
+ Dễ thấy rằng P cách nút gần nhất λ/8 → P dao động với biên độ
A P = 2 2 A b = 2 2 . 4 = 2 2 cm .
Điểm Q cách nút gần nhất một đoạn λ/8 → Q dao động với biên độ
A Q = 3 2 A b = 3 2 . 4 = 2 3 cm .
+ P và Q nằm trên các bó đối xứng nhau qua một nút nên dao động ngược pha nhau
→ khi P có li độ u p = A p 2 = 2 cm và hướng về vị trí cân bằng thì Q có li độ u Q = - A Q 2 = - 3 cm và cũng đang hướng về vị trí cân bằng.
→ Biểu diễn dao động của Q trên đường tròn. Từ hình vẽ, ta xác định được
∆ t = 0 , 25 T = 0 , 05 s .


Đáp án A
+ Biên độ dao động của phần tử dây cách nút một đoạn A M = A sin 2 π d λ : → A C = 2 2 A = 1 , 5 2 A D = A 2 = 1 , 5 cm.
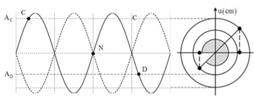
Ta chú ý rằng hai điểm C và D nằm ở hai bó sóng đối xứng nhau qua một nút do đó sẽ dao động ngược pha nhau → Tại thời điểm ban đầu t 0 , C đang ở biên dương cm thì khi đó D đang ở biên âm u D = − 1 , 5 2 cm
+ Khoảng thời gian ∆t ứng với góc quét φ = ω Δ t = 20 π + 3 π 4 → sau khoảng thời gian đó u D = 0 cm

Đáp án D
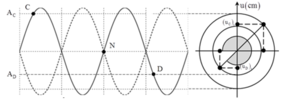
+ Biên độ dao động của các điểm cách nút một đoạn d khi có sóng dừng được xác định bởi A = A b sin 2 π d λ với A b là biên độ dao động của điểm bụng, vậy ta có:
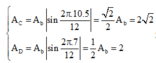
+ Hai điểm C và D thuộc bó sóng đối xứng với nhau qua nút N do vậy luôn dao động ngược pha nhau
+ Thời điểm t 0 C đang ở li độ
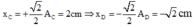
+ Góc quét tương ứng giữa hai thời điểm
![]()

Đáp án D
+ Biên độ dao động của các điểm cách nút một đoạn d khi có sóng dừng được xác định bởi
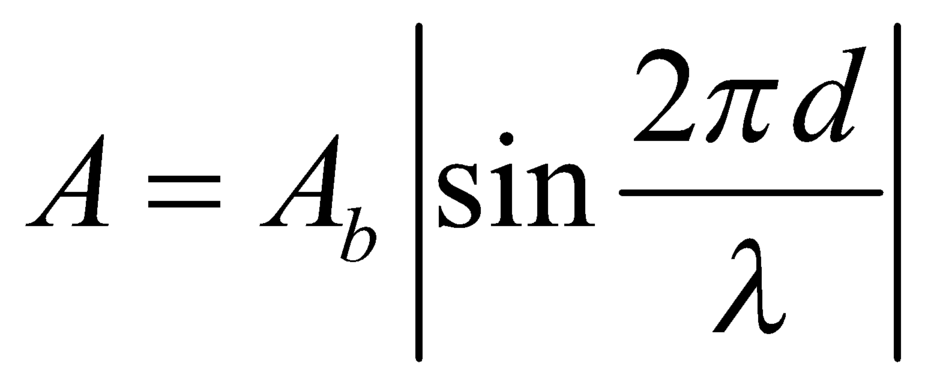
với ![]() là biên độ dao động của điểm bụng, vậy ta có:
là biên độ dao động của điểm bụng, vậy ta có:
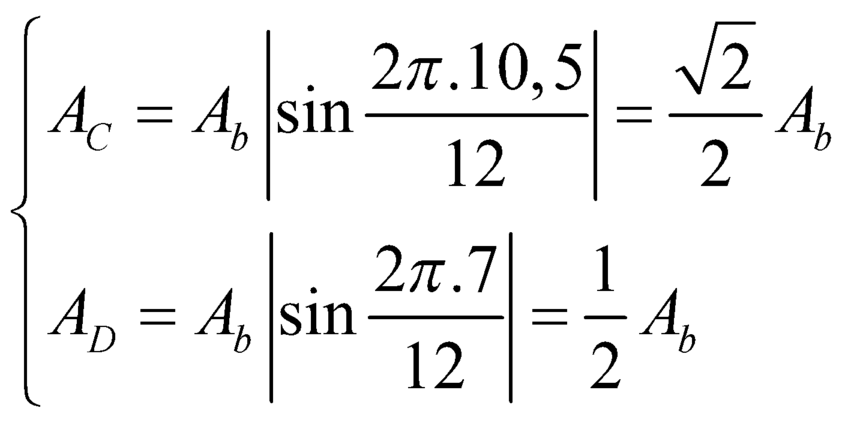
+ Hai điểm C và D thuộc các bó sóng đối xứng nhau qua nút N do vậy luôn dao động ngược pha nhau
+ Thời điểm ![]() C đang ở li độ
C đang ở li độ
![]()
+ Góc quét tương ứng giữa hai thời điểm
![]()

Đáp án D
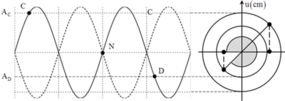
+ Biên độ dao động của các điểm cách nút một đoạn d khi có sóng dừng được xác định bởi A = A b sin 2 π d λ với Ab là biên độ dao động của điểm bụng, vậy ta có:
A c = A b sin 2 π 10 , 5 12 = 2 2 A b A D = A b sin 2 π 7 12 = 1 2 A b
+ Hai điểm C và D thuộc các bó sóng đối xứng nhau qua nút N do vậy luôn dao động ngược pha nhau
+ Thời điểm t 0 C đang ở li độ x c = + 2 2 A c ⇒ x D = - 2 2 A D
+ Góc quét tương ứng giữa hai thời điểm ∆ φ = ω ∆ t = 18 π + 1 , 75 π rad
⇒ x D = - A D = - 1 , 5 c m

Đáp án D
+ B là bụng thứ hai kể từ nút A → A B = λ 2 + λ 4 = 30 c m → λ = 40 cm
Chu kì của sóng T = λ v = 40 50 = 0 , 8 s
+ Biên độ dao động của của điểm C: A C = A B sin 2 π A C λ = 2 2 A B với A B là biên độ của điểm B.
→ Trong một chu kì khoảng thời gian giữa hai lần li độ của B bằng biên độ của C là Δt = 0,25T = 0,2 s.

Đáp án D
+ B là bụng thứ hai kể từ nút A → A B = λ 2 + λ 4 = 30 cm → λ = 40 cm.
Chu kì của sóng T = λ v = 40 50 = 0 , 8 s.
+ Biên độ dao động của của điểm C: A C = A B sin 2 π A C λ = 2 2 A B với A B là biên độ của điểm B.
→ Trong một chu kì khoảng thời gian giữa hai lần li độ của B bằng biên độ của C là Δ t = T 4 = 0 , 2 s.

Đáp án A
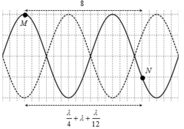
+ Từ giả thuyết của bài toán ta có thể xác định được điểm N cách nút một gần nhất một đoạn λ 12 , do đó N sẽ dao động với biên độ là 0,5A = 3 mm.
+ Tại thời điểm t, M đang chuyển động với tốc độ v N = v N m a x 2 = 6 π cm/s. Biểu diễn tương ứng trên đường tròn. Hai điểm M và N nằm trên hai bó sóng đối xứng với nhau qua một nút nên dao động ngược pha.
+ Từ hình vẽ ta có thể tính được, tại thời điểm , điểm N có gia tốc: a N = 3 2 a N max = 6 3 m / s 2
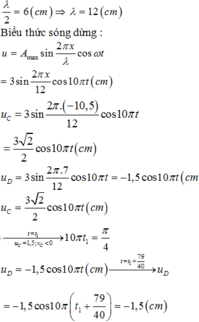
Đáp án D
+ Khoảng cách từ vị trí cân bằng của một nút đến một bụng gần nhất là một phần tư lần bước sóng → λ = 24 cm → Chu kì của sóng T = λ v = 0 , 24 1 , 2 = 0 , 2 s.
Biên độ dao động một điểm trên dây cách nút gần nhất một đoạn d được xác định bởi biểu thức a = A sin 2 π d λ → a P = 2 2 a Q = 2 3 cm.
+ Ta chú ý rằng P và Q nằm trên hai bó sóng đối xứng nhau qua một bó nên dao động cùng pha, tại thời điểm t, thì u P = a P 2 = 2 cm thì u Q = a Q 2 = 3 cm và cũng đang hướng về vị trí cân bằng.
→ Từ hình vẽ, ta thấy khoảng thời gian tương ứng sẽ là Δ t = 3 T 4 = 0 , 015 s