Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cạnh của hình vuông C1 là: a1 = 4 (giả thiết)
Giả sử cạnh hình vuông thứ n là an.
Theo định lý Py-ta-go : Cạnh hình vuông thứ n + 1 là :

⇒ (an) là cấp số nhân với a1 = 4 và công bội 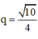

Diện tích ô vuông màu xanh sau lần phân chia thứ nhất là \(\frac{1}{9}\), số ô vuông màu xanh được tạo thêm là \({8^0}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ hai là \(\frac{1}{{{9^2}}}\), số ô vuông màu xanh được tạo thêm là \({8^1}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ ba là \(\frac{1}{{{9^3}}}\), số ô vuông màu xanh được tạo thêm là \({8^2}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ tư là \(\frac{1}{{{9^4}}}\), số ô vuông màu xanh được tạo thêm là \({8^3}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ ba là \(\frac{1}{{{9^5}}}\), số ô vuông màu xanh được tạo thêm là \({8^4}\).
Tổng diện tích các ô vuông màu xanh là
\(\frac{1}{9} + \frac{1}{{{9^2}}} \times {8^1} + \frac{1}{{{9^3}}} \times {8^2} + \frac{1}{{{9^4}}} \times {8^3} + \frac{1}{{{9^5}}} \times {8^4} = 0,445\).

a) Gọi \({u_n}\) là độ dài cạnh của hình vuông thứ \(n\).
Ta có: \({u_1} = 1;{u_2} = \frac{{{u_1}}}{2}.\sqrt 2 = \frac{{{u_1}}}{{\sqrt 2 }};{u_3} = \frac{{{u_2}}}{2}.\sqrt 2 = \frac{{{u_2}}}{{\sqrt 2 }};...\)
Từ đó ta thấy \(\left( {{u_n}} \right)\) là một cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \({u_n} = {u_1}.{q^{n - 1}} = 1.{\left( {\frac{1}{{\sqrt 2 }}} \right)^{n - 1}} = \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Diện tích của hình vuông thứ \(n\) là: \({a_n} = u_n^2 = {\left( {\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)^2} = \frac{1}{{{2^{n - 1}}}},n = 1,2,3,...\)
Vậy \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}}\)
Đây là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{2}\).
Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = 2\left( {1 - \frac{1}{{{2^n}}}} \right)\).
\(\lim {S_n} = \lim 2\left( {1 - \frac{1}{{{2^n}}}} \right) = 2\left( {1 - \lim \frac{1}{{{2^n}}}} \right) = 2\left( {1 - 0} \right) = 2\).
b) Chu vi của hình vuông thứ \(n\) là: \({p_n} = 4{u_n} = 4.\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Vậy \({Q_n} = 4 + \frac{4}{{\sqrt 2 }} + \frac{4}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 4\left( {1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)\)
\(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}\) là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 1.\frac{{1 - {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^n}}}{{1 - \frac{1}{{\sqrt 2 }}}} = \left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\).
\( \Rightarrow {Q_n} = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\)
\(\begin{array}{l}\lim {Q_n} = \lim 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right) = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \lim \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\\ & = 4\left( {2 + \sqrt 2 } \right)\left( {1 - 0} \right) = 4\left( {2 + \sqrt 2 } \right)\end{array}\).

Chọn D
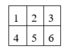
+ Tô màu ô vuông số 2: có C 3 2 cách chọn 2 trong 3 màu, có C 4 2 cách tô 2 màu đó lên 4 cạnh. Vậy có C 3 2 C 4 2 = 18cách.
+ Tô màu ô vuông số 1,5,3: có C 2 1 cách chọn màu còn lại, có C 3 2 cách tô màu còn lại lên 3 cạnh còn lại của 1 hình vuông. Vậy có ( C 2 1 C 3 2 ) 3 = 6 3 cách
+ Tô màu ô vuông số 4,6: Mỗi 1 hình vuông có 2 cách tô màu. Vậy có 2 2 = 4cách.
Vậy có 18. 6 3 .4 = 15552 cách thỏa mãn.

Chọn B
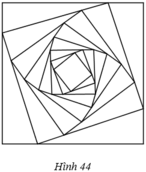
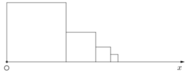
Tổng các cạnh nằm trên tia Ax của các hình vuông đó là
10 + 5 + 5 2 + 5 2 2 + . . . = 20 ( c m )

Đáp án B.
Tổng các cạnh nằm trên tia Ox của các canh hình vuông đó là:

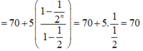

a) Ta có: \({u_1} = 1,{u_2} = 2,{u_3} = 3\)
Dự đoán \({u_n} = n\)
b) Ta có: \(\begin{array}{l}{v_1} = 1\\{v_2} = 8 = {2^3}\\{v_3} = 27 = {3^3}\\{v_4} = 64 = {4^3}\end{array}\)
Dự đoán: \({v_n} = {n^3}\)




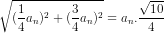 với n ε N*.
với n ε N*. 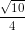

Ta có: \({u_1} = 1;{u_2} = 1;{u_3} = 2;{u_4} = 3;{u_5} = 5;{u_6} = 8;{u_7} = 13;{u_8} = 21\)
Ta có:
\(\begin{array}{l}{u_3} = 2 = {u_2} + {u_1}\\{u_4} = 3 = {u_3} + {u_2}\\{u_5} = 5 = {u_4} + {u_3}\\{u_6} = 8 = {u_5} + {u_4}\\{u_7} = 13 = {u_6} + {u_5}\\{u_8} = 21 = {u_7} + {u_6}\end{array}\)
Ta thấy dãy số này kể từ số hạng thứ 3 bằng tổng của hai số hạng đứng trước nó.
Vậy dãy số này có công thức truy hồi là:
\(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + {u_{n - 2}}\left( {n \ge 3} \right)\end{array} \right.\)