Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\widehat{MON}=\widehat{xOM}+\widehat{xON}=140^0+40^o=180^o\)
=> M; O; N thẳng hàng
=> MN cắt xx' tạo O => \(\widehat{xON};\widehat{x'OM}\) là hai góc đối đỉnh
![]() Cho đường thẳng xx' và một điểm O nằm trên đường thẳng xx'. Trên nửa mặt phẳng bờ xx', vẽ tia OM sao cho xOM =140% . Trên nửa mặt phẳng bờ xx' không chứa tia OM vẽ tia ON sao cho xON = 40%. chứng minh xON và x' OM là hai góc đối đỉnh.
Cho đường thẳng xx' và một điểm O nằm trên đường thẳng xx'. Trên nửa mặt phẳng bờ xx', vẽ tia OM sao cho xOM =140% . Trên nửa mặt phẳng bờ xx' không chứa tia OM vẽ tia ON sao cho xON = 40%. chứng minh xON và x' OM là hai góc đối đỉnh.![]()
∘

\(\widehat{MON}=\widehat{xOx'}-\widehat{xOM}-\widehat{NOx'}=180^o-30^o-30^o=120^o\)
\(\widehat{MOt}=\widehat{NOt}=\dfrac{\widehat{MON}}{2}=60^o\)
\(\Rightarrow\widehat{xOt}=\widehat{xOM}+\widehat{MOt}=30^o+60^o=90^o\Rightarrow ot\perp xx'\)

cửa hàng bán được một tạ rưỡi gẹo tẻ và gạo nếp ; trong đó 25% là gạo nếp. hỏi của hàng bán mỗi loại bao nhiêu ki-lô-gam gạo

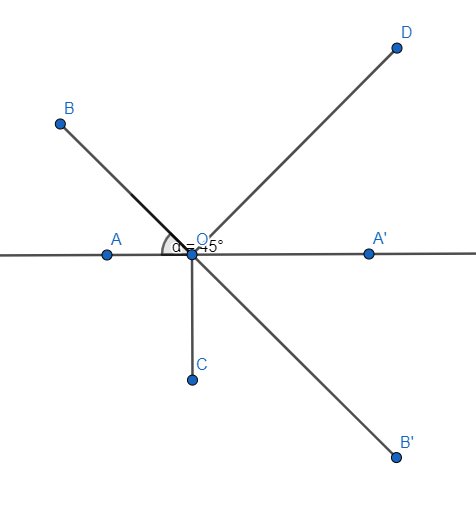
a) Vì OB' là tia phân giác của \(\widehat{A'OC}\) nên \(\widehat{A'OB'}=\dfrac{\widehat{A'OC}}{2}=\dfrac{90^o}{2}=45^o\). Suy ra \(\widehat{AOB}=\widehat{A'OB'}\left(=45^o\right)\). Lại có \(\widehat{AOB}+\widehat{BOA'}=\widehat{AOA'}=180^o\) nên \(\widehat{BOB'}=\widehat{A'OB'}+\widehat{BOA'}=180^o\) hay B, O, B' thẳng hàng. Suy ra \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là 2 góc đối đỉnh.
b) Trên cùng 1 nửa mặt phẳng bờ là đường thẳng AA', ta thấy tia OB nằm giữa 2 tia OA và OD, tia OD lại nằm giữa 2 tia OB và OA', do đó \(\widehat{AOB}+\widehat{BOD}+\widehat{DOA'}=\widehat{AOA'}\) \(\Leftrightarrow45^o+90^o+\widehat{A'OD}=180^o\) \(\Leftrightarrow\widehat{A'OD}=45^o\)

a/ Ta có:
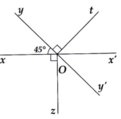
\(\widehat{yOz}=\widehat{xOy}-\widehat{xOz}=180^o-135^o=45^o\)
\(\widehat{xOt}=\widehat{xOy}-\widehat{yOt}=180^o-90^o=90^o\)
\(\Rightarrow\widehat{tOv}=\frac{\widehat{xOt}}{2}=\frac{90^o}{2}=45^o\)
Ta lại có:
\(\widehat{vOz}=\widehat{tOv}+\widehat{yOt}+\widehat{yOz}=45^o+90^o+45^o=180^o\)
\(\Rightarrow\widehat{vOz}\)là góc bẹt.
b/ Vì \(\widehat{vOz}\) là góc bẹt nên Oz và Ov là 2 tia đối nhau
Ta lại có Ox, Oy là 2 tia đối nhau nên suy ra \(\widehat{xOv},\widehat{yOz}\) là 2 góc đối đỉnh

Hình tự vẽ.
Giải:
\(\widehat{A'OB}=180^o-45^o=135^o\)
\(\widehat{A'OB'}=\frac{1}{2}\widehat{A'OC}=45^o\)
\(\Rightarrow\widehat{A'OB}+\widehat{A'OB'}=135^o+45^o=180^o\). Từ đây suy ra OB và OB' đối nhau.
Ta lại có OA và OA' đối nhau nên \(\widehat{AOB}\)và \(\widehat{A'OB'}\)đối đỉnh.
+) Tia OB nằm giữa 2 tia OA và OA' => góc AOB + BOA' = AOA' => 45 o + BOA' = 180 o => góc BOA' = 180 o - 45 o = 135 o
+) Tia OC nằm giữa 2 tia OA và OA' => góc A'OC + COA = AOA' => góc A'OC = 180 o - 90 o = 90 o
+) Tia OB' là tia p/g của góc A'OC => góc A'OB' = góc A'OC/2 = 45 o
và tia OB' nằm giữa 2 tia OA' và OC => tia OB' và OC nằm cùng nửa mp bờ chứa tia OA'
mà OC và OB nằm hai nửa mp bờ chứa tia OA'
=> tia OB' và OB nằm 2 nửa mp bờ chứa tia OA' => tia OA' nằm giữa 2 tia OB và OB'
=> góc BOA' + A'OB' = BOB'
=> 135 o + 45 o = BOB' => góc BOB' = 180 o => tia OB và OB' đối nhau mà 2 tia OA và OA' đối nhau
=> góc AOB và A'OB' đối đỉnh
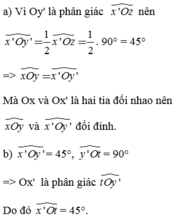
Ta có
\(\widehat{x'ON}=\widehat{xOx'}-\widehat{xON}=180^o-90^o=90^o\)
\(\Rightarrow\widehat{NOP}=\dfrac{\widehat{x'ON}}{2}=45^o\)
\(\Rightarrow\widehat{MOP}=\widehat{xOM}+\widehat{xON}+\widehat{NOP}=45^o+90^o+45^{^{ }o}=180^o\)
=> M; O; P thẳng hàng => MP cắt xx' tại O
\(\Rightarrow\widehat{xOM};\widehat{x'OP}\) là hai góc đối đỉnh
40
vì OP là tia p/giác của góc x'ON nên x'OP=x'ON:2 =90:2 =45 vây ta có xOM=x'OP=45 hay xOM đối đỉnh với x'OP