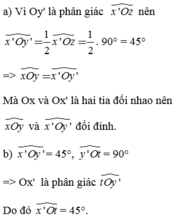Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

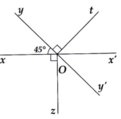
a) Vì Oy' là phân giác x ' O z ^ nên
x ' O y ' ^ = 1 2 x ' O z ^ = 1 2 . 90° = 45°
=> x O y ^ = x ' O y ' ^
Mà Ox và Ox' là hai tia đối nhau nên
x O y ^ và x ' O y ' ^ đối đỉnh
b) x ' O y ^ = 45°, y ' O t ^ = 90° => Ox' là phân giác t O y ' ^
Do đó x ' O t ^ = 45°
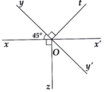

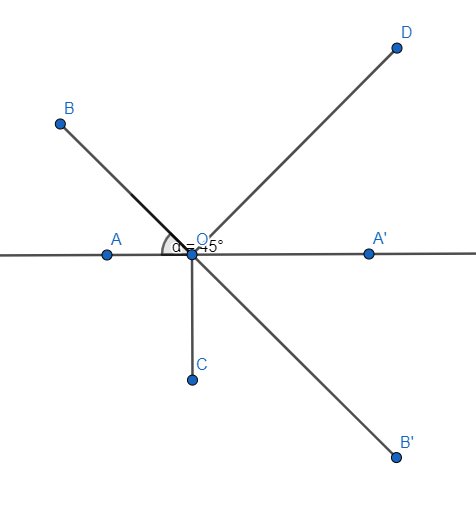
a) Vì OB' là tia phân giác của \(\widehat{A'OC}\) nên \(\widehat{A'OB'}=\dfrac{\widehat{A'OC}}{2}=\dfrac{90^o}{2}=45^o\). Suy ra \(\widehat{AOB}=\widehat{A'OB'}\left(=45^o\right)\). Lại có \(\widehat{AOB}+\widehat{BOA'}=\widehat{AOA'}=180^o\) nên \(\widehat{BOB'}=\widehat{A'OB'}+\widehat{BOA'}=180^o\) hay B, O, B' thẳng hàng. Suy ra \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là 2 góc đối đỉnh.
b) Trên cùng 1 nửa mặt phẳng bờ là đường thẳng AA', ta thấy tia OB nằm giữa 2 tia OA và OD, tia OD lại nằm giữa 2 tia OB và OA', do đó \(\widehat{AOB}+\widehat{BOD}+\widehat{DOA'}=\widehat{AOA'}\) \(\Leftrightarrow45^o+90^o+\widehat{A'OD}=180^o\) \(\Leftrightarrow\widehat{A'OD}=45^o\)

1.
Giải: a) Ta có: \(\widehat{xOy}+\widehat{yOx'}=180^0\) (kề bù)
=> \(\widehat{yOx'}=180^0-\widehat{xOy}=180^0-75^0=105^0\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOy}=75^0\) => \(\widehat{x'Oy'}=75^0\)
\(\widehat{yOx'}=\widehat{xOy'}\) (đối đỉnh)
Mà \(\widehat{yOx'}=105^0\) => \(\widehat{xOy'}=105^0\)
1b) Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\) (kề bù)
mà \(\widehat{x'Oy}-\widehat{xOy}=30^0\)
=> \(2.\widehat{x'Oy}=210^0\)
=> \(\widehat{x'Oy}=210^0:2=105^0\) => \(\widehat{x'Oy}=\widehat{xOy'}=105^0\) (đối đỉnh)
=> \(\widehat{xOy}=180^0-105^0=75^0\) => \(\widehat{xOy}=\widehat{x'Oy'}=75^0\) (đối đỉnh)
2.
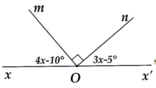
Giải: a) Ta có: \(\widehat{xOm}=\widehat{x'Om'}\) (đối đỉnh)
\(\widehat{mOy}=\widehat{m'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}\) (gt)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}.\widehat{xOy}\) (vì Om là tia p/giác)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}=\frac{1}{2}.\widehat{xOy}\)
=> Om' nằm giữa Ox' và Oy'
=> Om' là tia p/giác của góc x'Oy'
b) Tự viết

a) Ox' và Ox là hai tia đối nhau nên
\(\widehat{xOx'}=180^o\)mà \(\widehat{xOz}=90^o\)
\(\Rightarrow\widehat{x'Oz}=90^o\)
Mặt khác Oy' là tia phân giác của \(\widehat{x'Oz}\)
nên \(\widehat{x'Oy'}=\widehat{zOy'}=\frac{1}{2}\cdot90^o=45^o\)
\(\Rightarrow\widehat{x'Oy'}=\widehat{xOy}=45^o\)
Mà Ox' và Ox là 2 tia đối nhau, 2 tia Oy' và Oy thuộc 2 mặt phẳng đối nhau bờ là xx'
Do đó \(\widehat{x'Oy'}\)và \(\widehat{xOy}\)là 2 góc đối đỉnh. ( đpcm )
b) Ta có: Oy' và Oy là 2 tia đối nhau ( cmt )
\(\Rightarrow\widehat{yOt}+\widehat{tOy'}=180^o\)
\(\Rightarrow90^o+\widehat{tOy'}=180^o\)
\(\Rightarrow\widehat{tOy'}=90^o\)
Lại có Oy' và Oy thuộc 2 nửa mặt phẳng đối nhau bờ là xx' nên Ox' nằm giữa 2 tia Oy và Oy'
\(\Rightarrow\widehat{x'Ot}+\widehat{x'Oy'}=\widehat{tOy'}\)
\(\Rightarrow\widehat{x'Ot}+45^o=90^o\)
\(\Rightarrow\widehat{x'Ot}=45^o\)
Vậy \(\widehat{x'Ot}=45^o\)