Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Đặt log x = t, bất phương trình
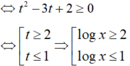
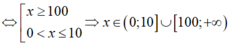
=> a + b + c =110.

Điều kiện: x>0
Vậy tích 2 nghiệm của phương trình là 20.
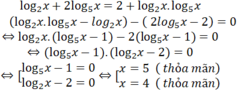
Chọn B.

Đáp án B
Phương pháp:
Đưa phương trình về dạng tích sau đó giải phương trình logarit cơ bản.
Cách giải:
ĐKXĐ: x > 0
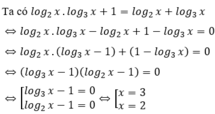
Tổng lập phương các nghiệm của phương trình là: 33 + 23 = 35

Chọn C.
Điều kiện x > 0
Phương trình tương đương:
log2x( log3x - 1) + x( log3x - 1) - 3(log3x - 1) = 0
Hay ( log3x - 1) ( log2 x + x - 3) = 0
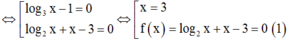
Ta có ![]() đồng biến với x > 0
đồng biến với x > 0
Suy ra (1) có nghiệm thì là nghiệm duy nhất, dễ thấy (1) có nghiệm x = 2
Suy ra 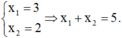

Chọn A.
Điều kiện x > 0.
Đặt t = log2x , phương trình trở thành : t2 + (x - 1) t + 2x – 6 = 0
Hay t2 – t – 6 + x(t + 2) = 0
(t + 2) (t - 3) + x(t + 2) = 0
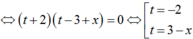
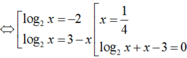
Xét hàm số f(x) = log2x + x - 3 với x > 0, có ![]()
Suy ra f(x) là hàm đồng biến trên khoảng ![]()
Khi đó phương trình f(x) = 0 có nhiều nhất một nghiệm trên khoảng ![]()
Mà f(2) = 0 nên x = 2 là nghiệm duy nhất của phương trình (*)
Vậy tổng các nghiệm của phương trình đã cho là 9/4.
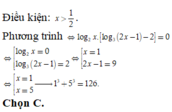

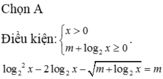
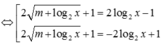
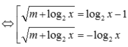

Chọn B
Tổng các nghiệm của phương trình là: 100+ 1= 101.