Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện x > 1. Khi đó phương trình tương đương với
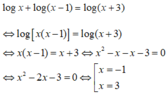
Loại nghiệm x = -1 do không thỏa mãn điều kiện. Phương trình có một nghiệm x = 3.
Chọn đáp án B.


ĐKXĐ: \(x>1\)
\(log_2\left(x-1\right)+log_2\left(x+1\right)=3\)
\(\Leftrightarrow log_2\left(x-1\right)\left(x+1\right)=3\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=8\)
\(\Leftrightarrow x^2-9=0\Rightarrow\left[{}\begin{matrix}x=3\\x=-3< 1\left(l\right)\end{matrix}\right.\)
Vậy tập nghiệm của pt là \(S=\left\{3\right\}\)


Lời giải:
$\log(8.5^x+20^x)=x+\log 25$
$\Rightarrow 8.5^x+20^x=10^{x+\log 25}=10^x.25$
$\Rightarrow \frac{8.5^x+20^x}{10^x}=25$
$\Leftrightarrow \frac{8}{2^x}+2^x=25$
Đặt $2^x=t$ thì $\frac{8}{t}+t=25$
$\Leftrightarrow t^2-25t+8=0$
Dễ thấy PT trên luôn có 2 nghiệm dương $t_1,t_2$ nên kéo theo PT ban đầu có 2 nghiệm $x_1,x_2$
Tổng các nghiệm $x_1+x_2=\log_2(t_1)+\log_2(t_2)=\log_2(t_1t_2)=\log_2(8)=3$

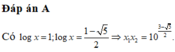
Đáp án B
Phương pháp:
Đưa phương trình về dạng tích sau đó giải phương trình logarit cơ bản.
Cách giải:
ĐKXĐ: x > 0
Tổng lập phương các nghiệm của phương trình là: 33 + 23 = 35