Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
Đặt \(\log_yx=a,\log_xy=b\). Khi đó ta có:
\(\left\{\begin{matrix} a+b=\frac{10}{3}\\ ab=\log_xy.\log_yx=1\end{matrix}\right.\)
Áp dụng định lý Viete đảo thì \(a,b\) là nghiệm của PT:
\(x^2-\frac{10}{3}x+1=0\) . PT trên có hai nghiệm \(3,\frac{1}{3}\)
Giả sử \(a=\log_yx=3\) và \(b=\log_xy=\frac{1}{3}\)
\(\left\{\begin{matrix} \log_y\left(\frac{144}{y}\right)=3\\ \log_x\left(\frac{144}{x}\right)=\frac{1}{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=24\sqrt{3}\\ y=2\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow \frac{x+y}{2}=13\sqrt{3}\). Đáp án D
Lời giải:
Đặt \(\log_{\frac{1}{2}}\sqrt{x+1}=t\Rightarrow \sqrt{x+1}=(\frac{1}{2})^t\)
\(\Rightarrow x+1=(\frac{1}{2})^{2t}=(2^{-1})^{2t}=2^{-2t}\)
\(\Rightarrow \log_2(x+1)=-2t\)
Vậy pt ban đầu tương đương với:
\(-2t+t=1\Leftrightarrow t=-1\)
\(\Rightarrow x+1=2^{-2t}=4\Rightarrow x=3\)
Lời giải:
Sử dụng công thức \(\log_ab=\frac{\ln b}{\ln a}\)
\(\Rightarrow A=\frac{\ln 2}{\ln 3}.\frac{\ln 3}{\ln 4}.\frac{\ln 4}{\ln 5}....\frac{\ln 15}{\ln 16}\)
\(\Leftrightarrow A=\frac{\ln 2}{\ln 16}=\log_{16}2=\frac{1}{4}\)
Đáp án C.
\(y'=-6x^2-6\left(2a+1\right)x-6a\left(a+1\right)\)
\(y'=0\Leftrightarrow x^2+\left(2a+1\right)x+a\left(a+1\right)=0\)
\(\Delta=\left(2a+1\right)^2-4a\left(a+1\right)=1>0\forall a\)
Ta có \(x_1+x_2=-\left(2a+1\right)\) và \(x_1x_2=a\left(a+1\right)\) (theo Vi-ét)
\(\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=...\)
1.\(\dfrac{log_ac}{log_{ab}c}=log_ac.log_c\left(ab\right)=log_ac.\left(log_ca+log_cb\right)=log_ac.log_ca+log_ac.log_cb=\dfrac{log_ac}{log_ac}+\dfrac{log_cb}{log_ca}=1+log_ab\)
2. \(log_{ax}bx=\dfrac{log_abx}{log_aax}=\dfrac{log_ab+log_ax}{log_aa+log_ax}=\dfrac{log_ab+log_ax}{1+log_ax}\)
3. \(\dfrac{1}{log_ax}+\dfrac{1}{log_{a^2}x}+...+\dfrac{1}{log_{a^n}x}=log_xa+log_xa^2+...+log_xa^n\)
\(=log_xa+2log_xa+...+n.log_xa=log_xa+2log_xa+...+n.log_xa\)
\(=log_xa.\left(1+2+...+n\right)=\dfrac{n\left(n+1\right)}{2}log_xa=\dfrac{n\left(n+1\right)}{2.log_ax}\)
Chọn C.
Điều kiện x > 0
Phương trình tương đương:
log2x( log3x - 1) + x( log3x - 1) - 3(log3x - 1) = 0
Hay ( log3x - 1) ( log2 x + x - 3) = 0
Ta có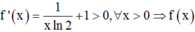
đồng biến với x > 0
Suy ra (1) có nghiệm thì là nghiệm duy nhất, dễ thấy (1) có nghiệm x = 2
Suy ra