Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TH1: m=-1/2
BPT sẽ là -2x-3/2-3>0
=>-2x>9/2
=>x<-9/4
=>Loại
TH2: m<>-1/2
Δ=(-2)^2-4(2m+1)(3m-3)
=4-4(6m^2-6m+3m-3)
=4-4(6m^2-3m-3)
=4-24m^2+12m+12
=-24m^2+12m+16
Để BPT vô nghiệm thì -24m^2+12m+16<=0 và 2m+1<0
=>m<-1/2 và \(\left[{}\begin{matrix}m< =\dfrac{3-\sqrt{105}}{2}\\m>=\dfrac{3+\sqrt{105}}{2}\end{matrix}\right.\)
=>\(m< =\dfrac{3-\sqrt{105}}{2}\)

Chọn B.
Đặt t= 5x> 0.
+ Phương trình đã cho trở thành: t2-( m+2) t+2m-1=0 suy ra 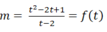 ( 2)
( 2)
( với t= 2 phương trình vô nghiệm).
Do đó phương trình đã cho có nghiệm khi phương trình (2) có nghiệm t> 0 .
+ Lập bảng biến thiên của hàm số f(t) dựa vào bảng biến thiên suy ra m ≤ 0 m ≥ 4
kết hợp điều kiện m nguyên và m ∈ [0;2018] => m ∈ {0;4;5;6;...;2018}
Vậy nghiệm 2016 giá trị của m thỏa mãn yêu cầu bài toán ra


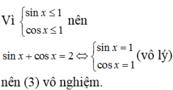



Áp dụng điều kiện có nghiệm của pt lượng giác bậc nhất, để pt đã cho vô nghiệm
\(\Leftrightarrow\left(2m+1\right)^2+\left(m+2\right)^2< \left(2m+3\right)^2\)
\(\Leftrightarrow5m^2+8m+5< 4m^2+12m+9\)
\(\Leftrightarrow m^2-4m-4< 0\)
\(\Leftrightarrow2-\sqrt{6}< m< 2+\sqrt{6}\)
\(\Rightarrow m=\left\{0;1;2;3;4\right\}\)
\(\Rightarrow\sum m=10\)