Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Với x ∈ 5 2 ; 4 thì phương trình tương đương với:
m - 1 log 2 2 x - 2 + m - 5 log 2 x - 2 + m - 1 = 0 (1)
Đặt log 2 ( x - 2 ) = t . Với x ∈ 5 2 ; 4 thì t ∈ - 1 ; 1 . Phương trình (1) trở thành:
( m - 1 ) t 2 + ( m - 5 ) t + m - 1 = 0 ⇔ m ( t 2 + t + 1 ) = t 2 + 5 t + 1 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 (2)
Xét hàm số f ( t ) = t 2 + 5 t + 1 t 2 + t + 1 = 1 + 4 t t 2 + t + 1 trên đoạn - 1 ; 1 .
Đạo hàm f ' ( t ) = - 4 ( t 2 - 1 ) t 2 + t + 1 ≥ 0 , ∀ t ∈ - 1 ; 1 ; f ' ( t ) = 0 ⇔ t = ± 1 . Khi đó hàm số f ( t ) đồng biến trên - 1 ; 1 . Suy ra min - 1 ; 1 f ( t ) = f ( - 1 ) = - 3 ; max - 1 ; 1 f ( t ) = f ( 1 ) = 7 3 .
Phương trình (2) có nghiệm ⇔ Đường thẳng y - m cắt đồ thị hàm số f ( t ) ⇔ - 3 ≤ m ≤ 7 3 . Vậy S = - 3 ; 7 3 → a = - 3 , b = 7 3 → a + b = - 3 + 7 3 = - 2 3 .

Ta có:
\(y'=x^2-2mx+m^2-4\)
\(y''=2x-2m,\forall x\in R\)
Để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đại tại x = 3 thì:
\(\left\{{}\begin{matrix}y'\left(3\right)=0\\y''\left(3\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+5=0\\6-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=1,m=5\\m>3\end{matrix}\right.\Leftrightarrow m=5\)
=> B.

\(f^2\left(\left|x\right|\right)-\left(m-6\right)f\left(\left|x\right|\right)-m+5=0\) có \(a-b+c=0\) nên có các nghiệm \(\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=m-5\end{matrix}\right.\)
- Với \(f\left(\left|x\right|\right)=-1\Rightarrow\left|x\right|^2-4\left|x\right|+3=-1\Rightarrow\left|x\right|=2\Rightarrow x=\pm2\) có 2 nghiệm
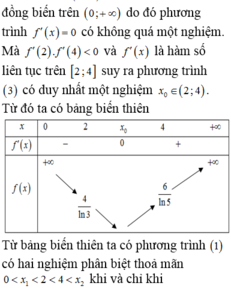
- Xét \(f\left(\left|x\right|\right)=m-5\Leftrightarrow\left|x\right|^2-4\left|x\right|+8=m\) (1)
Từ BBT của \(y=\left|x\right|^2-4\left|x\right|+8\) dễ dàng suy ra (1) có 4 nghiệm pb khi \(4< m< 8\)
\(\Rightarrow m=\left\{5;6;7\right\}\) có 3 giá trị nguyên

Đáp án D
Phương pháp:
Đặt 2x = t, t > 0. Chuyển về bài toán tìm m để phương trình bậc 2 ẩn t có 2 nghiệm t1, t2 thỏa mãn t1.t2 = 8
Cách giải:

Để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1 + x2 = 3 thì phương trình (2) có 2 nghiệm t1,t2 thỏa mãn t1.t2 = 2x1.2x2 = 2x1 + x2 = 23 = 8
Khi đó:
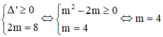
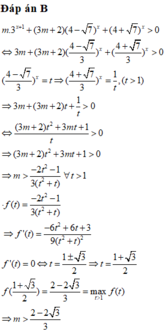


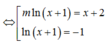
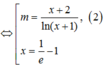

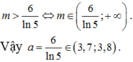




Đáp án B
n=1