DD
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
YN
4
HH
30 tháng 9 2019
A=2+2^2+2^3+....+2^10:3
A=(2+2^2)+(2^3+2^4)+....+(2^9+2^10):3
A=2.(1+2)+2^3.(1+2)+...+2^9.(1+2):3
A=2.3+2^3.3+...+2^9.3:3
A=3.(2+2^3+...+2^9):3
vậy A:3
10 tháng 12 2017
ta có: abcabc=abcx1000+abcx1=abcx(1000+1)=abcx1001=mà 1001 chia hết cho 11=>abcabc sẽ chia hết cho 11
Ta lại có: 1001 chia hết cho 7=>abcabc sẽ chia hết cho 7
CT
2
13 tháng 10 2018
115.
+) 312312 là một hợp số
Ta thấy 312 là 1 số chẵn nên 312 ít nhất là chia hết cho số 2, tưc là 312 có ước là 2 khác với 1 và 312. Nên 312 là một hợp số.
+) 213213 là một hợp số.
giải thích: tổng các chữ số của 213213 là 2+1+3=62+1+3=6 chia hết cho 33 nên 213213 ⋮⋮ 33, nghĩa là 213213 có ước là 33, khác 11 và 213213 do đó nó là hợp số .
+) 435435 là một hợp số
giải thích: 435435 có chữ số tận cùng là 55 nên 435435 ⋮⋮ 55 nghĩa là 435435 có ước là 55 khác 11 và 435435 do đó nó là hợp số.
+) 417417 là một hợp số.
giải thích: 417417 có tổng các chữ số là 4+1+7=124+1+7=12 chia hết cho 33 nên 417417 ⋮⋮ 33, nghĩa là 417417 có ước là 33, khác 11 và 417417 do đó nó là hợp số.
+) 33113311 là một hợp số.
giải thích: 3311=11.3013311=11.301 nên 33113311 có ước là 1111 và 301301. Vậy 33113311 là một hợp số.
+) 6767 là một số nguyên tố vì nó chỉ có hai ước là 11 và 6767.
116.
83∈P83∈P, (vì 8383 chỉ có hai ước là 11 và chính nó)
9191 ∉∉ PP, (vì 9191 có các ước 1,7,13,911,7,13,91 do đó nó không phải số nguyên tố)
15∈N15∈N,
P⊂NP⊂N. (dựa vào định nghĩa số nguyên tố là số tự nhiên chỉ có hai ước là 11 và chính nó).
120.
5∗5∗¯
∗∈{0,1,2,3,4,5,6,7,8,9}∗∈{0,1,2,3,4,5,6,7,8,9}
Do đó ta xét ∗∗ với từng giá trị
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯5∗5∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 5555 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 5151 có tổng các chữ số là 5+1=65+1=6 chia hết cho 33 do đó 5151 chia hết cho 33, trường hợp này loại
+) Nếu ∗=3∗=3 thì 5353 là số nguyên tố
+) Nếu ∗=7∗=7 thì 5757 có tổng các chữ số là 5+7=125+7=12 chia hết cho 33 do đó 5757 chia hết cho 33, trường hợp này loại.
+) Nếu ∗=9∗=9 thì 5959 là số nguyên tố.
Vậy * = {3; 9}
¯¯¯¯¯¯9∗9∗¯
Tương tự ta xét như trên và tìm được số 9797 là số nguyên tố.
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯9∗9∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 9595 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 9191 chia hết cho 77 do đó trường hợp này loại.
+) Nếu ∗=3∗=3 thì 9393 có tổng các chữ số là 9+3=129+3=12 nên chia hết cho 3 do đó 9393 là hợp số, do đó trường hợp này loại.
+) Nếu ∗=7∗=7 thì 9797 là một số nguyên tố.
+) Nếu ∗=9∗=9 thì 9999 là một hợp số vì cỏ tổng các chữ số là: 9+9=189+9=18 chia hết cho 33 và 99. Do đó trường hợp này loại.
Vậy * = 7
122.
a) Đúng, vì có 22 và 33 là hai số tự nhiên liên tiếp đều là số nguyên tố;
b) Đúng, đó là 3,5,73,5,7;
c) Sai, vì 22 là số chẵn đồng thời cũng là số nguyên tố;
d) Sai vì 22 cũng là số nguyên tố.
13 tháng 10 2018
Bài 115
312312 là một hợp số
Ta thấy 312 là 1 số chẵn nên 312 ít nhất là chia hết cho số 2, tưc là 312 có ước là 2 khác với 1 và 312. Nên 312 là một hợp số.
+) 213213 là một hợp số.
giải thích: tổng các chữ số của 213213 là 2+1+3=62+1+3=6 chia hết cho 33 nên 213213 ⋮⋮ 33, nghĩa là 213213 có ước là 33, khác 11 và 213213 do đó nó là hợp số .
+) 435435 là một hợp số
giải thích: 435435 có chữ số tận cùng là 55 nên 435435 ⋮⋮ 55 nghĩa là 435435 có ước là 55 khác 11 và 435435 do đó nó là hợp số.
+) 417417 là một hợp số.
giải thích: 417417 có tổng các chữ số là 4+1+7=124+1+7=12 chia hết cho 33 nên 417417 ⋮⋮ 33, nghĩa là 417417 có ước là 33, khác 11 và 417417 do đó nó là hợp số.
+) 33113311 là một hợp số.
giải thích: 3311=11.3013311=11.301 nên 33113311 có ước là 1111 và 301301. Vậy 33113311 là một hợp số.
+) 6767 là một số nguyên tố vì nó chỉ có hai ước là 11 và 6767.
Bài 116
83∈P83∈P, (vì 8383 chỉ có hai ước là 11 và chính nó)
9191 ∉∉ PP, (vì 9191 có các ước 1,7,13,911,7,13,91 do đó nó không phải số nguyên tố)
15∈N15∈N,
P⊂NP⊂N. (dựa vào định nghĩa số nguyên tố là số tự nhiên chỉ có hai ước là 11 và chính nó).
Bài 120
¯¯¯¯¯¯5∗5∗¯
∗∈{0,1,2,3,4,5,6,7,8,9}∗∈{0,1,2,3,4,5,6,7,8,9}
Do đó ta xét ∗∗ với từng giá trị
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯5∗5∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 5555 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 5151 có tổng các chữ số là 5+1=65+1=6 chia hết cho 33 do đó 5151 chia hết cho 33, trường hợp này loại
+) Nếu ∗=3∗=3 thì 5353 là số nguyên tố
+) Nếu ∗=7∗=7 thì 5757 có tổng các chữ số là 5+7=125+7=12 chia hết cho 33 do đó 5757 chia hết cho 33, trường hợp này loại.
+) Nếu ∗=9∗=9 thì 5959 là số nguyên tố.
Vậy * = {3; 9}
¯¯¯¯¯¯9∗9∗¯
Tương tự ta xét như trên và tìm được số 9797 là số nguyên tố.
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯9∗9∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 9595 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 9191 chia hết cho 77 do đó trường hợp này loại.
+) Nếu ∗=3∗=3 thì 9393 có tổng các chữ số là 9+3=129+3=12 nên chia hết cho 3 do đó 9393 là hợp số, do đó trường hợp này loại.
+) Nếu ∗=7∗=7 thì 9797 là một số nguyên tố.
+) Nếu ∗=9∗=9 thì 9999 là một hợp số vì cỏ tổng các chữ số là: 9+9=189+9=18 chia hết cho 33 và 99. Do đó trường hợp này loại.
Vậy * = 7
Bài 122
a) Đúng, vì có 22 và 33 là hai số tự nhiên liên tiếp đều là số nguyên tố;
b) Đúng, đó là 3,5,73,5,7;
c) Sai, vì 22 là số chẵn đồng thời cũng là số nguyên tố;
d) Sai vì 22 cũng là số nguyên tố.
k cho mk nha
G
3
TH
4
GR
27 tháng 12 2016
Gọi ƯCLN(2n+1;6a+4)=d
2n+1 \(⋮\) d\(\Rightarrow\) 6n +3\(⋮\) d
6n+4\(⋮\)d
\(\Rightarrow\)(6n+4)-(6n+3)\(⋮\) d
\(\Rightarrow\)6n+4 - 6n-3\(⋮\) d
\(\Rightarrow1⋮d\Rightarrow d=1\)
27 tháng 12 2016
Gọi d là ƯCLN (2a + 1; 6a + 4) Nên ta có :
2a + 1 ⋮ d và 6n + 4 ⋮ d
=> 3 ( 2a + 1 ) ⋮ d và 6n + 4 ⋮ d
=> 6a + 3 ⋮ d và 6a + 4 ⋮ d
=> (6a + 4) - (6a + 3) ⋮ d
=> 1 ⋮ d => d = 1
Vì ƯCLN (2a + 1; 6a + 4) = 1 => 2a + 1 và 6a + 4 là nguyên tố cùng nhau ( đpcm )
Cuối học kì I lớp 6 đề khó vậy !!
15 tháng 1 2016
CÁI NÀY CHỈ LÀ ĐỐ MẸO THÔI !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
GH
12 tháng 7 2023
\(S=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right).....\left(1-\dfrac{1}{2022}\right)\left(1-\dfrac{1}{2023}\right)\)
\(=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}....\dfrac{2022}{2023}\)
\(=\dfrac{1.2.3....2022}{2.3.4....2023}\)
\(=\dfrac{1}{2023}\)
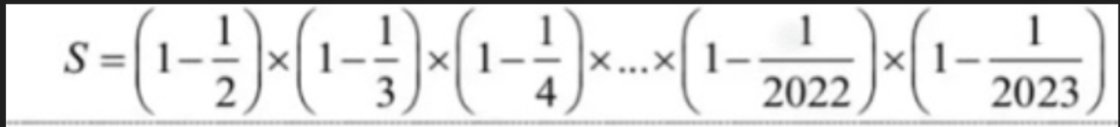
LÀM J CÓ DỞ HƠI
do bạn làm sai nên mới làm như vậy =))