Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Số phần tử của không gian mẫu ![]()
Gọi biến cố A: “Chọn được 1 bạn nam và 1 bạn nữ để phân công trực nhật.”
Ta có ![]()
Vậy ![]()

Số cách chọn 2 nữ từ 9 nữ: \(C_9^2\)
Số cách chọn 3 nam từ 8 nam: \(C_8^2\)
Hoán vị 5 bạn: \(5!\)
Vậy có \(5!.C_9^2.C_8^2\) cách

a. Có \(C_6^3\) cách chọn 3 nam từ 6 nam
b.
Chọn 2 nam từ 6 nam và 3 nữ từ 9 nữ để lập tổ 1 có: \(C_6^2.C_9^3\) cách
Chọn 2 nam từ 4 nam còn lại và 3 nữ từ 6 nữ còn lại để lập tổ 2 có: \(C_4^2.C_6^3\) cách
Chọn 2 nam từ 2 nan còn lại và 3 nữ từ 3 nữ còn lại: \(C_2^2.C_3^3\) cách
\(\Rightarrow C_6^2.C_9^3+C_4^2.C_6^3+C_2^2.C_3^3\) cách thỏa mãn chia 3 tổ

a) Nếu trong \(5\) học sinh phải có ít nhất \(2\) học sinh nữ và \(2\) học sinh nam thì có \(2\) trường hợp :
\(2\) nam \(3\) nữ, có : \(C^2_{10}.C^3_{10}\) cách:
\(3\) nam và \(2\) nữ, có : \(C^3_{10}.C^2_{10}\) cách:
Vậy tất cả có : \(2.C^2_{10}.C^3_{10}=10800\) cách.
b) Nếu trong \(5\) học sinh phải có ít nhất \(1\) học sinh nữ và \(1\) học sinh nam thì có 4 trường hợp :
\(1\) nam và \(4\) nữ, có: \(C^1_{10}.C^4_{10}\) cách.
\(2\) nam và \(3\) , có : \(C^2_{10}.C^3_{10}\) cách.
Còn lại bn tự lm nha, mỏi tay quá

Không gian mẫu là chọn ngẫu nhiên 5 học sinh từ 12 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 5 học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai . Ta mô tả các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Có bạn An.
Chọn thêm 2 học sinh nam từ 6 học sinh nam, có ![]() cách.
cách.
Chọn 2 học sinh nữ từ 4 học sinh nữ (không chọn Hoa), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Có bạn Hoa.
Chọn thêm 1 học sinh nữ từ 4 học sinh nam, có ![]() cách.
cách.
Chọn 3 học sinh nam từ 6 học sinh nam (không chọn An), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố là ![]()
Vậy xác suất cần tính 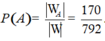
Chọn C.

