NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a)
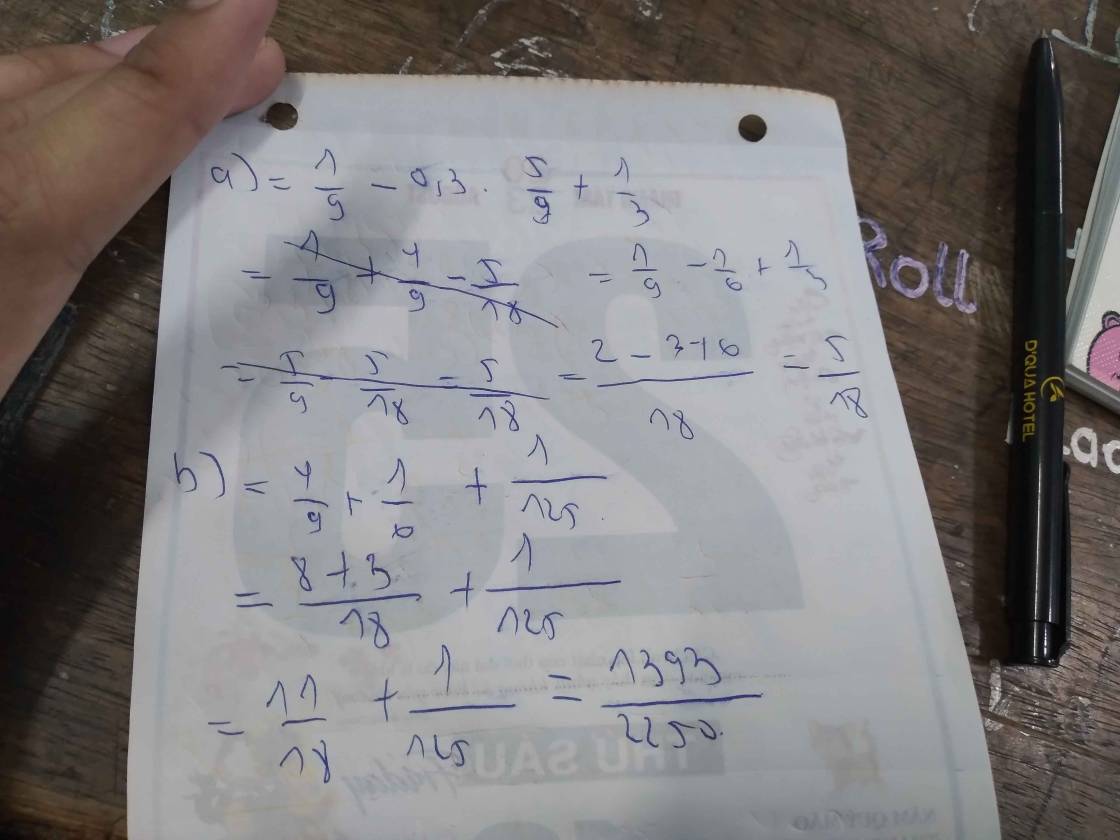
\(\begin{array}{l}\frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3}\\ = \frac{1}{9} - \frac{3}{{10}}.\frac{5}{9} + \frac{1}{3}\\ = \frac{1}{9} - \frac{3}{{2.5}}.\frac{5}{{3.3}} + \frac{1}{3}\\ = \frac{1}{9} - \frac{1}{6} + \frac{1}{3}\\ = \frac{2}{{18}} - \frac{3}{{18}} + \frac{6}{{18}}\\ = \frac{5}{{18}}\end{array}\)
b)
\(\begin{array}{l}{\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}\\ = \frac{4}{9} + \frac{1}{6} - \left( {\frac{{ - 1}}{2}} \right)^3\\ = \frac{4}{9} + \frac{1}{6} - \left( {\frac{{ - 1}}{8}} \right)\\ = \frac{4}{9} + \frac{1}{6} + \frac{1}{8}\\ = \frac{{32}}{{72}} + \frac{{12}}{{72}} + \frac{9}{{72}}\\ = \frac{{53}}{{72}}\end{array}\)
16 tháng 9 2023
a) `1/9-0,3. 5/9+1/3`
`=1/9-3/10 . 5/9+1/3`
`=1/9-15/90+1/3`
`=1/9-1/6+1/3`
`=2/18-3/18+6/18`
`=5/18`
b) `(-2/3)^2+1/6-(-0,5)^3`
`=4/9+1/6-(-0,125)`
`=4/9+1/6+0,125`
`=4/9+1/6+1/8`
`=32/72+12/72+9/72`
`=53/72`
NT
0
5 tháng 8 2023
a: |x+1|+(2y-1)^2=3
mà x,y nguyên
nên (2y-1)^2=1 và |x+1|=2
=>\(\left\{{}\begin{matrix}x+1\in\left\{2;-2\right\}\\2y-1\in\left\{1;-1\right\}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{0;-3\right\}\\y\in\left\{1;0\right\}\end{matrix}\right.\)
c: |3x-1|+|2y-5|=3
Th1: |3x-1|=0 và |2y-5|=3
=>3x-1=0 và 2y-5 thuộc {3;-3}
=>y thuộc {4;1}(nhận) và x=1/3(loại)
TH2: |3x-1|=1 và |2y-5|=2
=>3x-1 thuộc {1;-1} và 2y-5 thuộc {2;-2}
=>x thuộc {2/3;0} và y thuộc {7/2;3/2}
=>Loại
TH3: |3x-1|=2 và |2y-5|=1
=>3x-1 thuộc {2;-2} và 2y-5 thuộc {1;-1}
=>x=3 và y thuộc {3;2}
TH4: |3x-1|=3 và |2y-5|=0
=>3x-1 thuộc {3;-3} và 2y-5=0
=>y=5/2(loại)
d: |2x+1|+|y-5|=0
=>2x+1=0 và y-5=0
=>y=5(nhận) và x=-1/2(loại)
=>Ko có cặp số (x,y) nào thỏa mãn
DT
1
7 tháng 7 2016
Ta có :\(\frac{2a}{3}=\frac{3b}{4}=\frac{4c}{5}\)
\(\frac{a}{\frac{3}{2}}=\frac{b}{\frac{4}{3}}=\frac{2c}{\frac{5}{2}}\) \(=\frac{a-b+2c}{\frac{3}{2}-\frac{4}{3}+\frac{5}{2}}\)\(=\frac{6}{\frac{8}{3}}=\frac{9}{4}\)
\(\begin{cases}a=\frac{27}{8}\\b=3\\c=\frac{45}{8}\end{cases}\)
12 tháng 11 2021
c: \(=\dfrac{3}{2}\cdot1-1-20=\dfrac{3}{2}-21=\dfrac{-39}{2}\)
NV
6
IM
27 tháng 11 2016
Ta có :
a:b:c=3:4:5
\(\Rightarrow\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
Đặt \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=k\)
\(\Rightarrow\begin{cases}a=3k\\b=4k\\c=5k\end{cases}\)
Thay vào biểu thức ta được :
\(\frac{5a^2+2b^2-c^2}{2a^2+3b^2-2c^2}=\frac{5.9.k^2+2.16.k^2-25.k^2}{2.9.k^2+3.16.k^2-2.25.k^2}=\frac{k^2\left(45+32-25\right)}{k^2\left(18+48-50\right)}=\frac{52}{16}=\frac{13}{4}\)
a) \(\left(2.5\right)^3=10^3=1000\)
b) \(\left(3\frac{1}{2}\right)^2=\left(\frac{7}{2}\right)^2=\frac{49}{4}\)
c) \(\left(\frac{1}{5}\right)^5.5^5=\frac{1}{3125}.3125=\frac{3125}{3125}=1\)